Written by Volodymyr Proshkin, an academic visitor of the Department of Mathematics Education at Loughborough University. The sphere of his research interests includes the issues of teaching and learning mathematics, improving students’ science and mathematics literacy, and using digital technologies in education. For more information about Volodymyr and his work, there is a link at the end of this blogpost. Edited by Dr Bethany Woollacott.

This blogpost is based on a recent paper given by Volodymyr Proshkin with Mariia Astafieva, Dmytro Bodnenko and Oksana Lytvyn at the conference “ICT in Education, Research and Industrial Applications” (Ukraine, 18-22.09.2023). This study examines the utilization of the Learning Management System ‘Moodle’ as a platform for facilitating independent student learning by applying a metacognitive approach, in the context of physical and mathematical disciplines. This paper is linked at the end of the blogpost.

Effective learning during students’ independent study

Effective independent study is an essential prerequisite for successful learning. This issue becomes especially relevant when students are engaged in blended or distance learning.

Thanks to the development of digital technology, internet platforms have become an integral feature of the modern educational process. One such platform is the Learning Management System ‘Moodle’, which has a wide functionality for organizing independent work and is free, open-source and used by many universities.

Within Moodle, teachers can create Forums about a specific topic to hold asynchronous discussions with their students. As such, Moodle can be used to:

• facilitate communication between teachers/lecturers and students;
• make announcements to a whole class;
• facilitate discussions about course content, study materials, or problematic issues;
• design non-standard activities, e.g., ‘puzzles’ for students to discuss and solve together.

However, effective, targeted use of Moodle requires not only knowledge of the platform’s functionality and technical skills in using its tools but also a metacognitive approach to learning.

Why is the metacognitive approach critical in organizing students’ independent study in mathematics?

The metacognitive approach is based on developing cognitive skills that allow students to learn and control their learning independently. Metacognitive approaches support students in organising their independent work by enabling them to plan, manage and evaluate their learning.

The specificity of mathematical disciplines (e.g., the high level of abstraction or the logic, interconnectedness and interdependence of various topics) dictates the need for specific metacognitive strategies for successful learning. Some examples of metacognitive strategies are:

• conceptual understanding, not memorising by rote;
• predicting a hypothesis and searching for ways to prove or refute it, not passively familiarising self with a hypothesis;
• verifying a solution, not just stating an answer.

Therefore, we decided to investigate how Moodle facilitates metacognitive approaches within students’ self-learning strategies, and their lecturer’s teaching strategies. In the following, we present a specific case study, focusing on the metacognitive approaches which emerged whilst a lecturer was using Moodle with their class.

Example of using Moodle to organize students’ independent study

In the Forum of the e-learning Moodle course, “Strong planimetric nuts”, first-year students-mathematicians of Borys Grinchenko Kyiv University were asked to solve 32 planimetric tasks (i.e., tasks about 2D measurements). The tasks had non-standard or unusual conditional formula. In the Forum of the e-learning Moodle course, “Strong planimetric nuts”, first-year students-mathematicians of Borys Grinchenko Kyiv University were asked to solve 32 planimetric tasks (i.e., tasks about 2D measurements). The tasks had non-standard or unusual conditional formula.

---

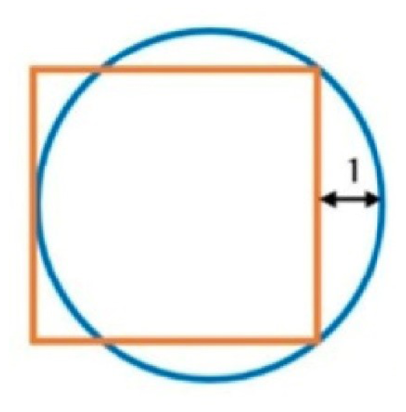
One student wrote: “How can you solve such problems if almost nothing is known? I don’t even know where to start”.

---

The lecturer took advantage of the situation to develop students’ thinking and metacognition. In the Forum, the lecturer chose the task depicted above and invited students to either ask questions to be given more information (which was initially hidden) or offer a solution.

The picture below demonstrates the discussion groups trying to find a solution.

Some students have suggested ‘using the sine theorem’ or the ‘Pythagoras’ theorem’ and they can then discuss whether this is likely to help them ascertain the answer within the relevant discussion page.

When posting a solution on the Forum, students had to briefly (in one phrase) indicate the method or key idea of the solution – a strategy which is one of the important cognitive abilities for self-learning.

The lecturer’s metacognitive strategy was to encourage observation by helping students to ask the right questions, and use the Moodle tool, creating an atmosphere of excitement and competition. The lecturer also initiated the meta-cognitive strategy of reflection, encouraging students to discuss the proposed solutions, reflect on their thinking, describe and analyse the search for the idea of a solution, and evaluate their own cognitive experiences.

---

Another student made a reflection which suggested that they were aware of their metacognitive strategy of performing additional constructions to see the solution:

“At first glance, it seemed that the problem could not be solved because insufficient information was given. But, considering various variants of additions, a rectangular triangle immediately struck me, from which, according to Pythagoras’ theorem, it is easy to find the side of the square.”

---

Summary

This blogpost aimed to illustrate how Moodle can support students’ independent work in mathematics and facilitate metacognitive approaches, by initiating strategies to encourage reflection, search for solutions, and evaluate their cognitive experiences. Future research should endeavour to evaluate the efficacy of Moodle tools as a priority, to support situations of remote learning.