Written by Dr Tom Francome and Dr Dave Hewitt. Tom is a PGCE tutor and a Senior Enterprise Fellow at the Centre for Mathematical Cognition at Loughborough University. He currently researches the nature of practising in mathematics, early algebra, and curriculum design. Dave is a visiting academic in the Department of Mathematics Education after recently retiring from a long career as a teacher educator. Dave’s research centres around the notion of the economic use of time and effort in the teaching and learning of mathematics, with particular interest in the teaching of algebra, early number, and the use of technology. For more information about Tom, Dave, and their work, there is a link at the end of this blogpost. Edited by Dr Bethany Woollacott.

Algebra is often seen as a hard to teach topic particularly for some groups of learners but do there have to be difficulties? The Centre for Mathematical Cognition funded a newly developed version of the software Grid Algebra which is now freely available and linked at the end of this blogpost. The software is very visual and involves representing physical movements on the grid with formal notation, providing an intuitive approach to number and early algebra work. In this blog we offer a brief background to some of the issues the software is designed to address and the theoretical underpinnings. Grid Algebra can be used for working with the whole class ‘economically’ using Hewitt’s¹ ideas of subordination to work on formal algebraic notation. This blog might be useful even if you’ve never used Grid Algebra, but you are interested in supporting all learners to think algebraically.

The structure of the grid and how Grid Algebra works

The foundation of school algebra rests on the extension and generalisation of the four mathematical operations of addition, subtraction, multiplication, and division. This is inherent within Grid Algebra which is based on the familiar multiplication grid. The image below shows a section of the multiplication grid in Grid Algebra.

In Grid Algebra, the four fundamental mathematical operations can be seen through physical movement: you can rub out numbers in cells, you can colour cells in, and you can drag numbers onto the grid from a list of numbers – numbers will only be accepted onto the grid if they are the correct number for that cell, giving implicit feedback to allow users to consider why a rejected number is not accepted. The grid size can also be changed to show a larger or smaller portion of the grid.

Although initial focus is on numbers in the grid, using the software can shift attention onto the relationships between the numbers. This shifts attention from numbers to operations. How would you get from 3 to 4? This could be done in several ways but the most straightforward is to add one and drag the 3 in row 1 one cell to the right which would result in 3+1 appearing in the 4 cell. Movements to the right are consistently represented as additions, irrespective of the row being considered. However, the row’s importance becomes apparent as moving one cell to the right in row 3 implies adding three instead of just one, as we are moving in the three times table. Subtraction is the inverse of addition, and this corresponds to the inverse movement to the left instead of the right. Consequently, learners’ natural understanding of the inverse relationship between movement and its corresponding operation can aid in comprehending the inverse relationship between arithmetic operations. Movements up and down the grid correspond to division and multiplication respectively and movements right and left correspond to addition and subtraction.

---

“Although initial focus is on numbers in the grid, using software can shift attention onto the relationships between the numbers“

---

A key aspect of Grid Algebra is that expressions can be created by dragging. A new expression can, in turn, be dragged around to make expressions of increasing complexity where each one movement corresponds to one operation. The formal notation offers a record of the journey taken on the grid. For example, the journey below shows number 3 in row 1 moving two to the right, down to row 4, three to the left, and then up to row 2, resulting in the expression which appears in the cell currently marked 4 in row 2.

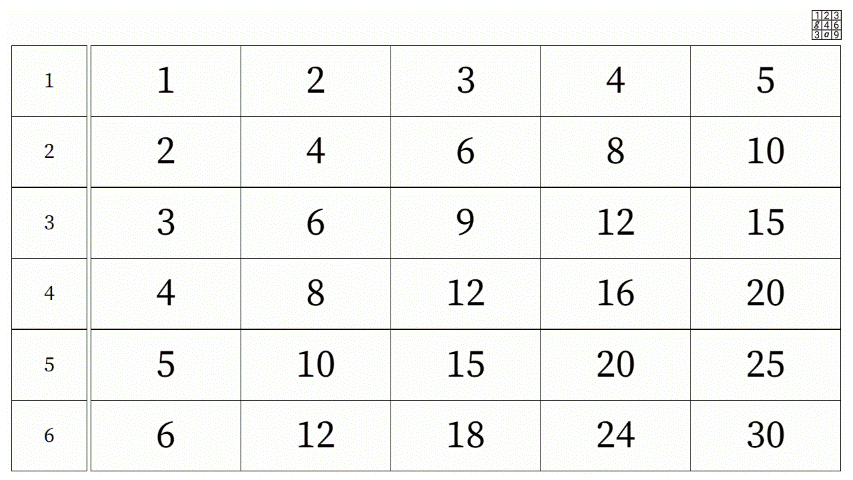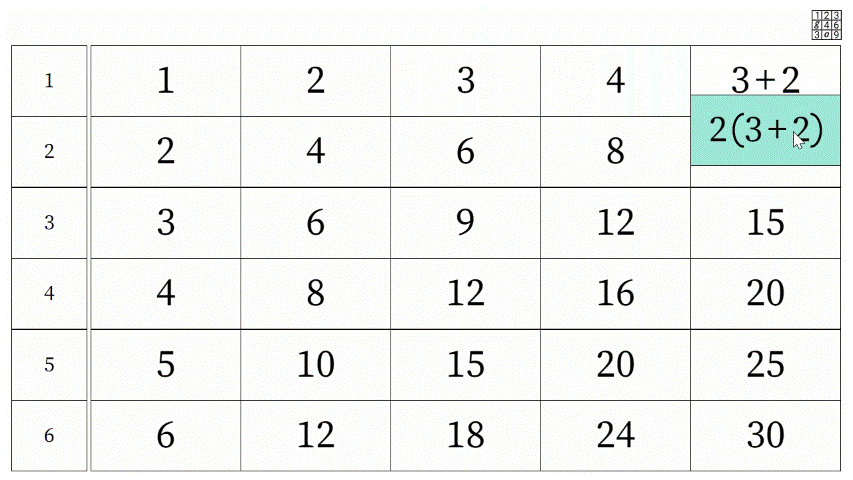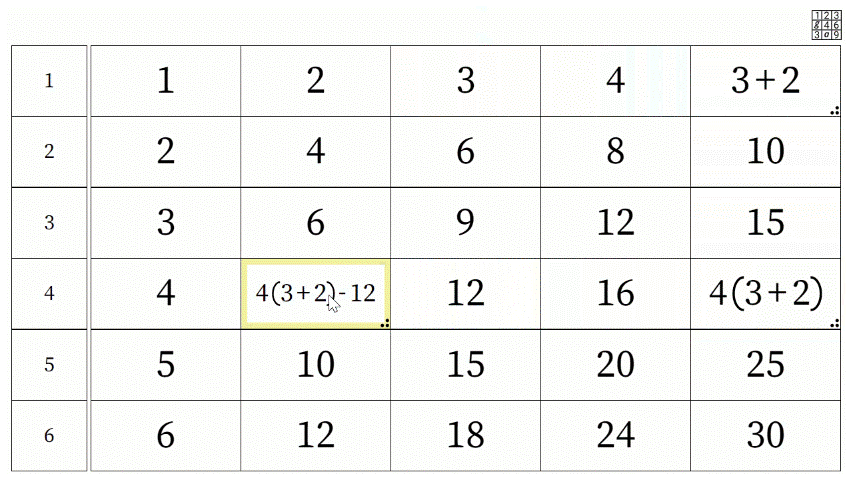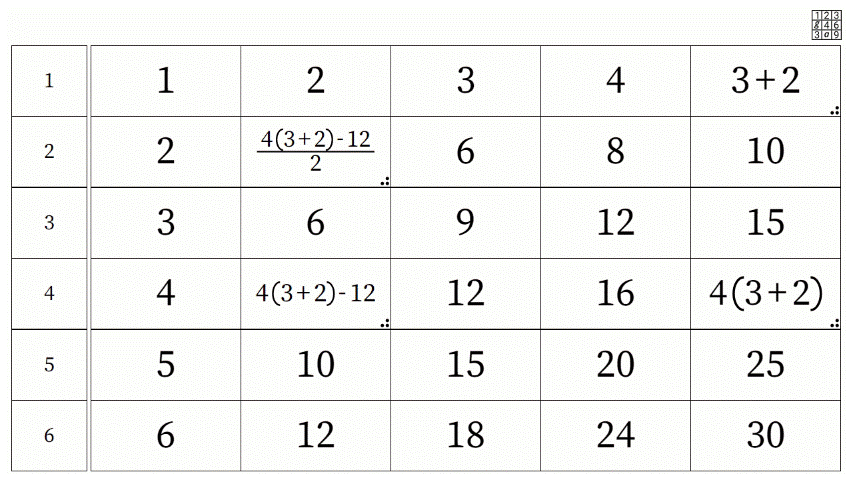
In algebra, the introduction of letters can be problematic², however, Grid Algebra can smooth the transition from numbers to letters as attention is shifted to the operations and away from the starting number such that the starting number begins to take a placeholder role, to be later replaced by a starting letter. Further work with the software can focus on the order of operations, equivalent expressions, factorising, expanding brackets, inverse operations, and solving equations (see below).

The research behind Grid Algebra

Research over many decades has shown that students have difficulty with learning algebra² and that the way algebra is taught may contribute to these difficulties³. Since initial findings in the eighties, more recent work in 2009 suggested little had changed in the intervening thirty years⁴. There is evidence that classroom level interventions can increase algebraic proficiency⁵ and furthermore that Grid Algebra is beneficial for vulnerable groups^6,7. Evidence from the past four decades has identified consistently positive benefits of digital technologies⁸ and Grid Algebra, in particular, has been proven to improve students’ understanding of letters⁹ and enabled primary-aged children to become confident with letters in formal algebraic notation as they learn to solve linear equations¹⁰. It is in this context that this accessible free software was developed ‘democratizing access to big ideas’¹¹.

We would encourage you to use the button at the end of this blogpost to head to our website and have a play with Grid Algebra (a freely available resource). This will give you the best understanding of the grid and the affordances of the software for developing an understanding of number and early algebra. The software relates to a variety of number work, such as: multiples, factors, primes, common multiples, common factors and negative numbers. It then builds on number work to address early algebra topics such as: introducing formal notation, letters, substitution, expanding brackets, factorising, equivalent expressions, inverse operations and solving linear equations.

The website includes an introduction to the software through videos and the supporting resources include lesson plans and student worksheets. There is an opportunity for free play in the Grid Algebra environment and to engage with the many computer-generated tasks which are available. Algebra is often seen as a ‘hard to teach topic’ but exploring formal notation with Grid Algebra has the potential to make learners more competent and confident with early algebra.

---

“Algebra is often seen as a ‘hard to teach’ topic but exploring formal notation with Grid Algebra has the potential to make learners more competent and confident with early algebra“

---

The resource is freely available having been funded by Loughborough’s Centre for Mathematical Cognition.

References

¹Hewitt, D. (1996). Mathematical fluency: The nature of practice and the role of subordination. For the Learning of Mathematics, 16(2), 28–35.

²Kuchemann, D. E. (1980). The Understanding of Generalised Arithmetic (Algebra) by Secondary School Children [PhD Thesis]. University of London.

³Macgregor, M., & Stacey, K. (1997). Students’ understanding of algebraic notation: 11-15. Educational Studies in Mathematics, 33(1), 1–19. https://doi.org/10.1023/A:1002970913563

⁴Hodgen, J., Kiichemann, D., Brown, M., & Coe, R. (2009). Children’s understandings of algebra 30 years on. Research in Mathematics Education, 11(2), 193–194. https://doi.org/10.1080/14794800903063653

⁵Hodgen, J., Coe, R., Brown, M., & Küchemann, D. (2014). Improving students’ understanding of algebra and multiplicative reasoning: did the ICCAMS intervention work? Pope, S. (Ed.) Proceedings of the 8th British Congress of Mathematics Education 2014. https://nottingham-repository.worktribe.com/OutputFile/727048

⁶Borg, P. (2019). Using the computer as a tool for constructivist teaching : a case study of Grade 7 students developing representations and interpretations of mathematical notation when using the software Grid Algebra. PhD Thesis, University of Loughborough

⁷Lugalia, M. (2015). Pupils learning algebra with ict in key stage 3 mathematics classrooms [University of Warwick]. In PQDT – UK & Ireland. http://webcat.warwick.ac.uk/record=b2827363~S1

⁸Higgins, S., Katsipataki, M., Villanueva-Aguilera, A. B., Coleman, R., Henderson, P., Major, L. E., Coe, R., & Mason, D. (2016). The Sutton Trust-Education Endowment Foundation Teaching and Learning Toolkit. Education Endowment Foundation. http://dro.dur.ac.uk/20987/

⁹Jones, I., Bisson, M., Gilmore, C., & Inglis, M. (2019). Measuring conceptual understanding in randomised controlled trials: Can comparative judgement help? British Educational Research Journal, 45(3), 662–680.

¹⁰Hewitt, D. (2012). Young students learning formal algebraic notation and solving linear equations: Are commonly experienced difficulties avoidable? Educational Studies in Mathematics, 81(2), 139–159. https://doi.org/10.1007/s10649-012-9394-x

¹¹Kaput, J. (1995). Long term algebra reform: Democratizing access to big ideas. In C. Lacampagne, W. Blair, & J. Kaput (Eds.), The algebra initiative colloquium (Vol. 1, pp. 33–49). U.S. Department of Education. https://files.eric.ed.gov/fulltext/ED385436.pdf#page=37