“If at first you don’t succeed”: An example of how early years practitioners encourage children to try again in mathematics learning interactions.
Written by Natalie Flint, Postdoctoral Research Associate at the Centre for Early Mathematics Learning (CEML). Her interests are in how learning interactions unfold in early years education settings. There is a link to the CEML website at the end of this blogpost for more information about the research happening in the centre or details about how to get involved. Edited by Dr Bethany Woollacott.
This blogpost is based on ongoing work and presents some preliminary findings from an ongoing CEML research project. To learn more about this research as it progresses, please follow Natalie’s ongoing work at CEML using the links at the bottom of this blogpost.
Introduction
“If at first you don’t succeed, try, and try again” is a classic idiom that conceptualises a general attitude to how we approach hurdles and barriers throughout our lives. Moments which could potentially be interpreted as ‘failures’ are to be reinterpreted as ’learning opportunities’ – particularly in education contexts. Here, we explore how Early Years practitioners encourage children to try again in mathematics learning interactions.
The Science of Conversation
Conversation Analysis is a systematic method used for analysing ordinary, naturally occurring interactions, focussing on action, or what we do with words, and sequence, or the organisation and structure of talk. Through the analysis of action and sequence, we can learn how real interactions unfold (see Clift, 2016).
“Conversation Analysis is a systematic method used for analysing ordinary, naturally occurring interactions, focussing on action, or what we do with words,and sequence, or the organisation and structure of talk.“
In the study we discuss here, we used Conversation Analysis to evaluate the interactions children in the early years were having with practitioners, their families, their peers, and the world around them. In particular, we explored a specific interactional moment in mathematics learning interactions: what do practitioners do to encourage children to try again? We analysed video data from naturally occurring preschool/classroom interactions in English education settings with 3–4-year-old children. Conversation Analysis enabled us to examine exactly how these children’s learning interactions played out.
How to Encourage a Child to Try Again
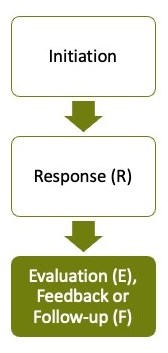
To examine how these interactions unfold, we consider interactions to comprise a number of ‘moves’ framed as IRE or IRF patterns, exemplified in the diagram here. IRE and IRF patterns are well-documented in education (see Mehan, 1979; Sinclair & Coulthard, 1975).
In our study, we were interested in what can happen in the third turn (highlighted in the diagram): once a practitioner has initiated and a child has given an incorrect response, how does the practitioner encourage the child to provide another response and try again? This classic structure is typical in early years classrooms, but advice on how to formulate evaluations, feedback and follow-up in early years contexts is scarce. Our study aimed to capture some of this feedback to understand which types of feedback are most effective in encouraging a child to ‘try again’.
The following example exemplifies an IRE/IRF pattern observed over multiple extracts. In this particular extract, two teachers are sat with a group of children at the start of the day for circle time and have just talked about the day of the week and the date. Teacher-1 initiates with a question about what month they are in. (Talk transcribed in square brackets “[ ] “ is spoken in overlap).
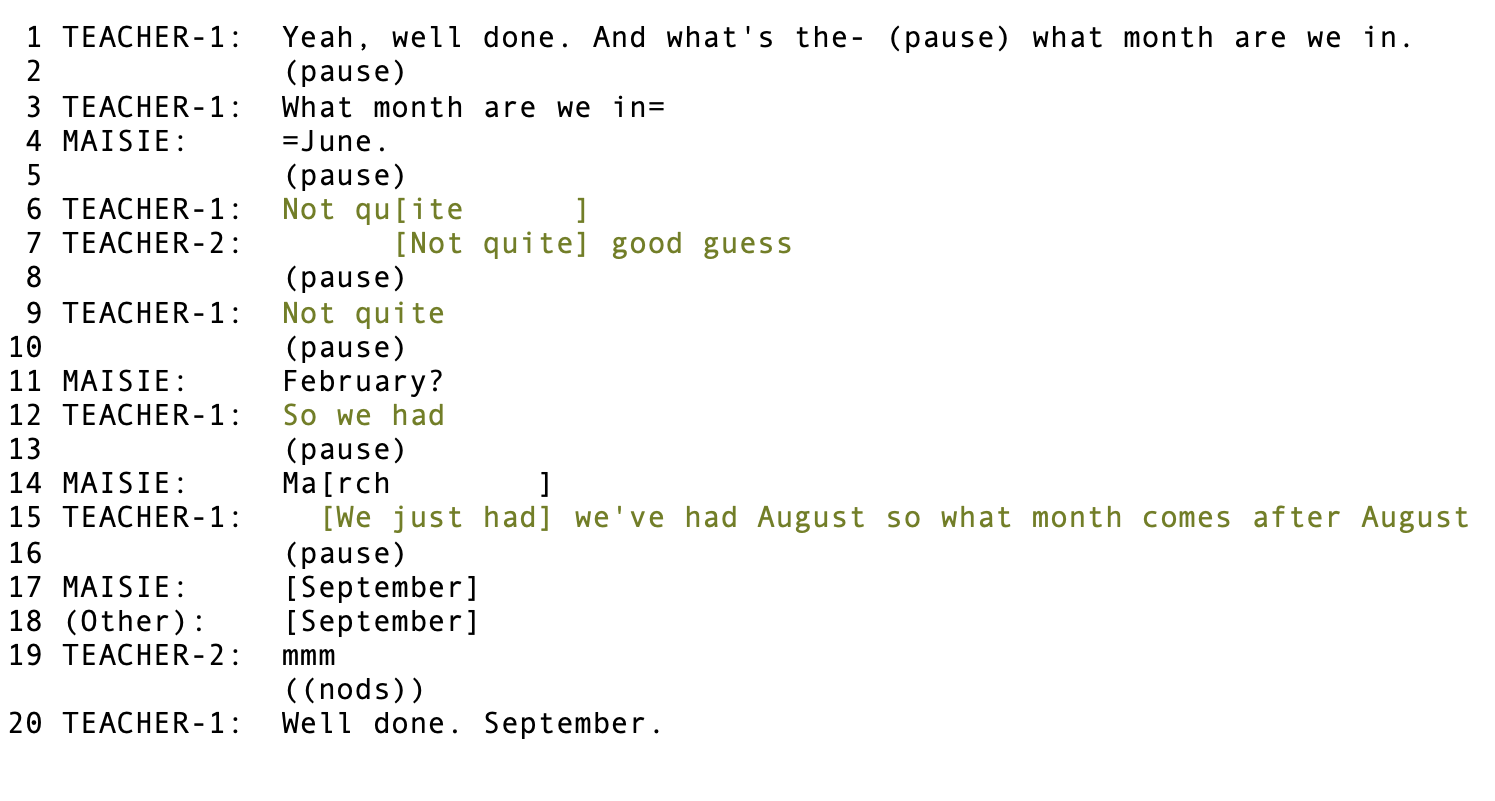
Here, the IRE/IRF sequence is initiated by teacher who asked the group “what month are we in”. One child, Maisie, responds quickly (as is illustrated in the transcript by “=”), with a month, but not the month they are currently in. It is at this point that we see some evaluation, feedback or follow-up. Both teachers give feedback which is encouraging and supportive at lines 6-9.
Their initial feedback to Maisie’s answer acknowledges that Maisie’s attempt is of the right category of answer (i.e., Maisie answers “June” rather than “Monday”). The teachers do not attempt to correct Maisie, which often occurs when an answer is treated as a typical repair (i.e., some issue with speaking, hearing or understanding that participants aim to deal with as swiftly as possible – which we see in all types of talk – not just in interactional contexts or with children). Instead, they simply acknowledge the attempt and evaluate it.
Following this initial evaluation of her first answer, Maisie attempts again. After another attempt from Maisie, the teacher begins to give feedback which scaffolds and guides the child to getting the answer (although this is initially cut off as Maisie attempts a third guess). After more than one attempt, the teacher provides feedback which prompts Maisie to draw on a particular area of knowledge. Here, Teacher-1 reminds Maisie of the name of the previous month, thus encouraging her to orient to her knowledge of the sequence of the months of the year. This prompt requires the children to do more than ‘guess’ by naming a month, but instead prompts them to remember sequences and patterns that they might know. This prompt encourages Maisie to draw on this area of knowledge, thus leading to her (and another child) to getting the answer at lines 17-18. Following this answer, Teacher-1 praises the child for finding the answer and repeats the answer.
In sum, the teacher offers encouraging support following the first attempt, and scaffolding encouragement following further attempts. And it is this that ultimately encourages the child to find the answer. Once the child reaches the answer, the teacher gives praise and confirms the answer.
“…the teacher offers encouraging support following the first attempt, and scaffolding encouragement following further attempts.“
Upgrading Feedback
The IRE/IRF structure is one that may be familiar to many practitioners. However, knowing how to give useful feedback that encourages children to try again can be difficult to navigate. Here we recognise a pattern of initial encouraging feedback that does not attempt to guide or scaffold after a first attempt, and further feedback that guides and scaffolds the child to find the answer after another attempt.
In this example, the teacher gives encouraging feedback which allows the child to try again, and following another attempt, provides a reformulated question which scaffolds the child to find the answer for themselves. This practice allows the child to find the answer by providing additional information so that the child can use this information and work out the answer.
We want to thank the nurseries/schools, practitioners, and children for participating in this research. We are grateful to the educational practitioners with whom we co-designed the game, and those who helped with the piloting phase. This work was partially supported by UKRI Economic and Social Research Council [grant number ES/W002914/1]).
References
Clift, R. (2016). Conversation Analysis. Cambridge University Press.
Mehan, H. (1979). Learning Lessons. Harvard University Press.
Centre for Mathematical Cognition
We write mostly about mathematics education, numerical cognition and general academic life. Our centre’s research is wide-ranging, so there is something for everyone: teachers, researchers and general interest. This blog is managed by Joanne Eaves and Chris Shore, researchers at the CMC, who edits and typesets all posts. Please email j.eaves@lboro.ac.uk if you have any feedback or if you would like information about being a guest contributor. We hope you enjoy our blog!