Written by Bobo Kai Yin Chan, a third-year doctoral researcher at the Department of Mathematics Education, Loughborough University. Bobo has a psychology degree and a master’s degree in applied psychology. Her research interests include cognitive load theory, spaced practice/spacing effect, and educational psychology. Edited by Dr Bethany Woollacott.

This blogpost reviews existing literature on spacing and interleaving research. Bobo is currently supervised by Dr Ouhao Chen and Dr Hugues Lortie-Forgues, with this meta-analysis mainly supported by Dr Lortie-Forgues.

Introduction

Researchers are keen to look for ways to improve mathematics performance and achievement. Spaced and interleaved practice are two approaches which aim to improve learning by considering how learning materials are connected and distributed across learning sessions. Both approaches typically work well in mathematics education as well as other areas of learning (such as memorising words and rules, and learning languages^3,5).

In this blog post, I discuss existing spacing and interleaving research in mathematics education and general education. I also highlight the importance of collecting together all the evidence from previous studies via a meta-analysis, aiming to understand the general effectiveness of spacing and interleaving practices for mathematics achievement.

What is spaced practice, interleaved practice and blocked practice, and how do they affect mathematics learning?

Spaced practice refers to inserting a time gap between learning sessions.

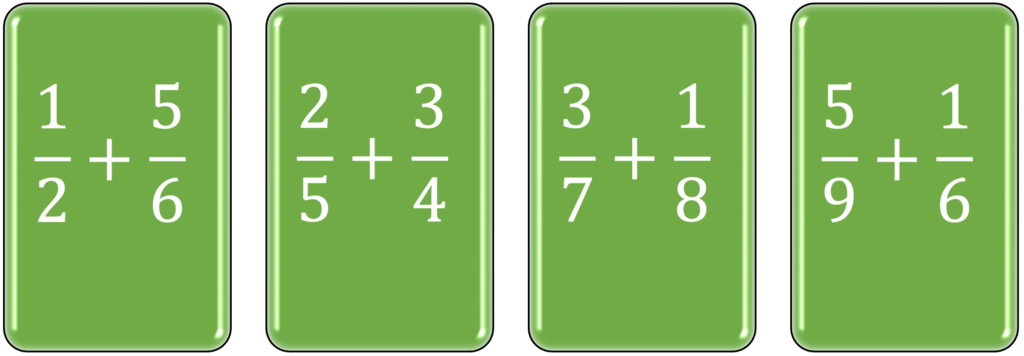
Blocked practice refers to doing similar problems in the same learning sessions; a learning session following a blocked practice approach is exemplified in the green diagram below. Reproduced from Weinstein et al.¹⁰.

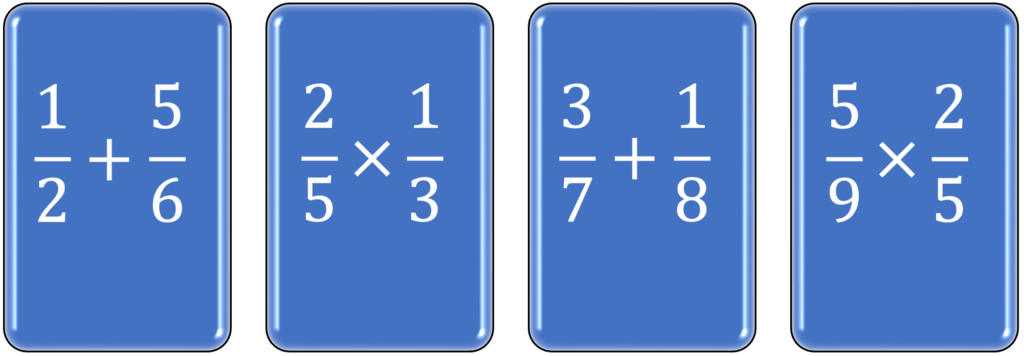
Interleaved practice refers to intermixing similar problems across different learning sessions; a learning session following an interleaved practice approach is exemplified in the blue diagram below. Reproduced from Weinstein et al.¹⁰.

These effects have been comprehensively researched and found to be effective for learning and retaining knowledge in various subject areas, including paired-associate tasks (e.g., pairing vocabulary with its meaning) and memory tasks³.

Previous research has indicated that both spaced and interleaved practices could yield positive effects for mathematics learning and other domains. In mathematics education research, more research has investigated the effectiveness of interleaved practice compared to spaced practice; I review the existing evidence for each type of practice next.  

Existing evidence on spaced and interleaved practices in non-mathematical domains

There are multiple meta-analyses (collections of evidence from previous studies) documenting spaced and interleaved practices in non-mathematical domains.

One meta-analysis conducted on spaced practice focusses on how the use of spacing impacts learning a second language. The results of this meta-analysis revealed that learners who learnt by spacing new vocabulary recalled more words than those who learnt the same new vocabulary without spacing⁵ (i.e., massed practice).

Another meta-analysis compared spaced and massed practice in 271 verbal memory tasks (e.g., memorising and recalling vocabulary), specifically investigating the effect of distributed practice and lag effects. Distributed practice refers to separating learning into two or more sessions using temporal gaps between sessions, while lag effects refers to the impact of differing lengths of spacing used between learning sessions (where longer spaces typically results in better learning than shorter ones). The results of this meta-analysis found a significant difference in learning when spacing the verbal memory tasks, suggesting that distributed practice is useful for memorising and recalling vocabulary. In addition, lag effects were found to benefit learning when the intervals between learning sessions were at least a day to three months, rather than intervals spaced within the same day.

For interleaved practice, Brunmair and Richters’ meta-analysis examined the effectiveness of interleaving in various domains, including paintings, mathematical tasks, artificial pictures, expository texts, words, and tastes¹. Their findings suggest that interleaved practice might not be beneficial for learning words (unlike spacing) but could be advantageous for classifying paintings. Their results also suggest a small benefit of using interleaved practice during mathematical tasks.

Existing spaced practice research in mathematics education

Based on the aforementioned information, the spacing effect appears effective in tasks that heavily rely on memorizing words, rules, and language learning. However, mathematics demands more than just memorizing terms; it also requires learners to select the correct strategies to solve mathematical problems and to use the correct procedures to calculate the answers². Therefore, although the spacing effect could be potentially beneficial for mathematics learning, the complexity of learning mathematics goes beyond memorising words or learning grammatical rules.

---

“However, mathematics demands more than just memorizing terms…“

---

Studies investigating spaced practice in mathematics have generated mixed results.

One study with students aged 8 to 10 suggested that students might benefit from spaced practice when learning mathematical words⁶. Similarly, a recent study involving students aged 12 to 13, compared spaced and massed practices when calculating basic probability and permutation problems. The study revealed that students who engaged in spaced practice demonstrated superior post-test scores and more accurate predictions about their performance on the post-test than the students who engaged in the massed practice⁴.

However, spacing practice is not always effective for learning. For instance, another study investigated the effectiveness of spaced practice with undergraduate students, comparing spaced and massed practices by asking students to solve some permutation problems. All students took two post-tests one week and five weeks after the final practice session. The results suggested that students might only benefit from spaced learning when learning conceptual knowledge but not when learning procedural knowledge⁹.

Existing interleaved practice research in mathematics education

As previously mentioned, there are comparatively more studies investigating interleaved practice in mathematics education compared to spaced practice.

Several studies have investigated interleaved practice in mathematics learning by interleaving similar problems or topics. For example, a study with students aged 12 to 13 involved the students solving the same practice algebraic problems over 3 months except that one group were given the problems via an interleaved approach and the other group via a blocked approach. Students were tested on their algebraic skill at the end of the 3 months and then again 1 month later. Results suggested that students learning via the interleaved approach solved more problems correctly at both time points compared to the blocked group⁸.

However, another study found that interleaved practice was not beneficial for students of a similar age learning mathematics. Students aged 10 to 12 were given some practice problems to develop their knowledge of fractions. Students once again were split into two groups where one group were given the problems structured using an interleaving approach, and the other group given the problems structured using a blocked approach. Results revealed no significant differences between students’ learning, irrespective of whether they completed the problems via an interleaved or blocked approach or whether students had low or high prior knowledge⁷. Therefore, it remains inconclusive whether interleaved practice is beneficial for mathematics achievement.

---

“…it remains inconclusive whether interleaved practice is beneficial for mathematics achievement.“

---

Since the results of previous studies were inconclusive, it is essential to gather evidence to find the overall impact of spaced and interleaved practices in mathematics education, including their impact on mathematics achievement and the possible factors influencing both effects. As part of my PhD, we are currently conducting a meta-analysis to systematically determine the effects of spaced and interleaved practices on mathematics achievement.

Conclusion

Previous research has suggested that spaced and interleaved practices might be beneficial to some subject areas, like memory tasks and classifying paintings. However, there seems to be inconclusive evidence that either spaced or interleaved practices benefit mathematics learning. As such, we are currently conducting a meta-analysis to fully understand the current evidence on the effects of spaced and interleaved practice on mathematics achievement.

References

1. Brunmair, M., & Richter, T. (2019). Similarity Matters: A Meta-Analysis of Interleaved Learning and Its Moderators. Psychological Bulletin, 145(11), 1029–1052. https://doi.org/10.1037/bul0000209

2. Munoz-Rubke, F., Vera-Bachmann, D., & Alvarez-Espinoza, A. (2019). Learning math: Two principles to avoid headaches. Frontiers in Psychology, 10(SEP), 1–5. https://doi.org/10.3389/fpsyg.2019.02042

3. Cepeda, N. J., Pashler, H., Vul, E., Wixted, J. T., & Rohrer, D. (2006). Distributed practice in verbal recall tasks: A review and quantitative synthesis. Psychological Bulletin, 132(3), 354–380. https://doi.org/10.1037/0033-2909.132.3.354

4. Emeny, W. G., Hartwig, M. K., & Rohrer, D. (2021). Spaced mathematics practice improves test scores and reduces overconfidence. Applied Cognitive Psychology, 35(4), 1082–1089. https://doi.org/https://doi.org/10.1002/acp.3814

5. Kim, S. K., & Webb, S. (2022). The Effects of Spaced Practice on Second Language Learning: A Meta-Analysis. Language Learning, 72(1), 269–319. https://doi.org/10.1111/lang.12479

6. Petersen-Brown, S., Lundberg, A. R., Ray, J. E., Dela Paz, I. N., Riss, C. L., & Panahon, C. J. (2019). Applying spaced practice in the schools to teach math vocabulary. Psychology in the Schools, 56(6), 977–991. https://doi.org/10.1002/pits.22248

7. Rau, M. A., Aleven, V., & Rummel, N. (2010). Blocked versus interleaved practice with multiple representations in an intelligent tutoring system for fractions. Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 6094 LNCS(PART 1), 413–422. https://doi.org/10.1007/978-3-642-13388-6_45

8. Rohrer, D., Dedrick, R. F., & Stershic, S. (2015). Interleaved practice improves mathematics learning. Journal of Educational Psychology, 107(3), 900–908. https://doi.org/10.1037/edu0000001

9. Ebersbach, M., & Barzagar Nazari, K. (2020). No robust effect of distributed practice on the short- and long-term retention of mathematical procedures. Frontiers in Psychology, 11(April), 1–9. https://doi.org/10.3389/fpsyg.2020.00811

10. Weinstein, Y., Madan, C. R., & Sumeracki, M. A. (2018). Teaching the science of learning. Cognitive Research: Principles and Implications, 3(1). https://doi.org/10.1186/s41235-017-0087-y