This blogpost was written by Saf Shah, a PhD student investigating mathematics undergraduates’ conceptions of intuition and rigour.  Saf has been at the DME since 2020, and his PhD supervisors are Dr. Paola Iannone, Prof. Lara Alcock, Prof. Ian Jones, and Dr. Fenner Tanswell.  There are links to learn more about Saf’s work, and the work of his supervisors, at the bottom of the blogpost. Edited by Dr. Bethany Woollacott.

In this blog post, Saf reviews the literature on the role of explanation and its relationship to proof. Saf starts by reporting theoretical research into the purposes and roles of explanation and how it relates to instruction in undergraduate mathematics.  This is followed by reporting two empirical studies investigating undergraduate students’ understandings of proofs, which can give insights into undergraduates’ engagement with proof validation and construction and the explanatory role of proof.

Introduction

There is much research into the different roles of proof in undergraduate mathematics¹. These roles can be more than simply verifying a mathematical statement (verification), including explanation, communication, and discovery¹. In this blog post, I focus on explanation.

Theoretical Research

Mathematicians often use proofs to gain insights into conjectures and to comprehend the underlying reasons behind their validity. According to Rota², while verification is an aspect of proof, it may not “necessarily provide a reason” (ibid., p. 186) as to why a theorem statement is correct. Therefore, appealing to reason or explanations is crucial in mathematical practice³. Hanna⁴ distinguishes between proofs that confirm and proofs that explain, arguing that solely using syntactic methods (using quantifiers and formal language) does not often provide a rationale based on underlying mathematical ideas and, thus, is not explanatory. Practising mathematicians value proof as a tool for conceptual understanding – like an explanation – rather than just correct syntactical derivations (i.e., using first-order logic)^4,5.

---

“According to Rota, while verification is an aspect of proof, it may not “necessarily provide a reason” (ibid., p. 186) as to why a theorem statement is correct.“

---

The Role of Mathematical Proofs in Teaching Undergraduates

In the context of undergraduate mathematics instruction, proofs should be presented and described considering the level of detail, classroom context, and students’ experience⁶. Explanatory proofs can take various forms, such as a calculation, a visual demonstration, or a guided discussion, depending on the grade level and instructional context⁶. Hanna⁴ suggests that the challenge for students is understanding the accuracy of known results and why they are true. Students can gain insight by relating mathematical statements to specific examples, facilitating the transition from procedural to conceptual knowledge^7,8. Additionally, specific proof methods, such as proving through contradiction or mathematical induction, may verify but not explain.  As such, it is essential for instructors to carefully select examples of proof to enable undergraduates to gain insights into the underlying reasoning in proofs and gain explanations from them.

---

“Explanatory proofs can take various forms, such as a calculation, a visual demonstration, or a guided discussion, depending on the grade level and instructional context.“

---

Below is a visual proof as an example of the explanatory role of proof.

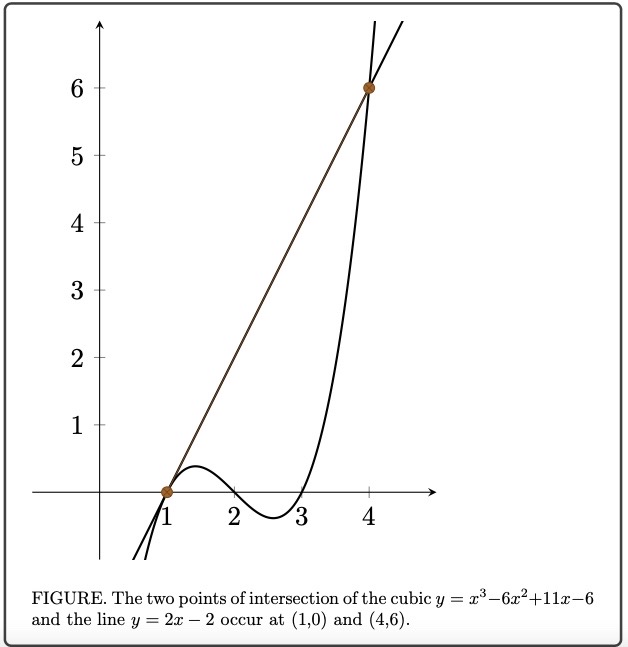
Empirical Research

A large body of existing empirical research relates formal proof (in the educational sense) to its role as being explanatory^7,9. In this review, I present the results of two empirical studies (a mixed methods study and a qualitative study) to illustrate the main findings within the corpus of research literature on the explanatory role of proof in undergraduate mathematics.  The findings presented are corroborated by other studies in this domain¹⁰. 

Firstly, Stylianou and colleagues¹¹ investigated students’ beliefs about proof relating to the roles of verification, explanation, and communication.  The authors used mixed methods and asked 535 undergraduate students to (i) complete a multiple-choice test and (ii) a questionnaire. The multiple-choice test was designed to ask students what constitutes proof and their thoughts on its role in mathematics – it also asked students to evaluate simple proofs to check their competency. The questionnaire (again multiple-choice) aimed to elicit students’ beliefs about proof and their previous classroom experience with proof.  60 of the 535 students also participated in a written test. The written test asked students to construct proofs for conjectures included in the multiple-choice test.  Then, finally, out of the 60 students who completed the written test, 40 were interviewed for 30 minutes using a list of carefully prepared questions.

The findings suggest that students have a double conception of proof: proof arguments that they thought would receive the best mark or proof arguments that they would adopt for themselves (ibid.). Further, the authors found that students did not perceive symbolic-deductive arguments (e.g., proof by contradiction) as explanatory and saw proofs explained in words as explanatory.  This finding suggests that semantic parts of a formal proof can help undergraduate students derive explanations – from such statements, which is significant in the context of university education.  If semantic arguments can facilitate proof validation (and production) within a proof and are seen as being explanatory, then engaging with such arguments can act as a bridge to better understanding the overall reasoning of a given argument or proof.

A second study by Simon and Blume¹² corroborated the finding that engaging with proving (e.g., validating proofs) can aid in understanding the overall reasoning in a given proof and help gain insight. The authors presented research from a three-year project with prospective elementary school teachers’ mathematical and pedagogical development in a teacher preparation program. The authors interviewed 26 prospective teachers and found that validating and constructing proofs helped the participants gain insight into the underlying reasoning in the given proofs. Participants could create and validate their ideas relating to proof and develop understanding by engaging in the justification of mathematical conjectures and statements. The study also found that conceptual understanding affected what participants accepted as a valid justification. When participants justified their answers, they relied on explaining procedures and their appropriateness, which helped students gain insight into the procedures and concepts being explored. This study found that when participants aimed to justify conjectures, this activity developed insight and resulted in learning (ibid.).

Although both studies addressed the need for proofs to be explanatory, neither investigated the potential context dependency of the proofs presented. It is plausible to assume one proof may be explanatory for one student while not for another due to contextual factors (e.g., targeted audience, conventions of writing proofs in sub-disciplines, etc.). For example, a proof may be relevant for publication and explanatory within the relevant mathematical communities, while the same proof may not be explanatory to undergraduate students. Therefore, contextual factors relating to explanatory proofs within undergraduate mathematics need further empirical research.  My PhD research is focused on exploring undergraduate students’ awareness of this explanatory role of proof by presenting them with a visual proof from Ording¹³.

Summary

In this blog post, I have concentrated on presenting theoretical and empirical research into the explanation role of proof. The theoretical research shows that proofs can provide insight and explain why a theorem is true. The literature surrounding instruction in undergraduate mathematics suggests that teaching explanatory proofs allows the learner to gain further insights into proof beyond verification. The two empirical studies that I have presented here corroborate this view and further show the value of explanatory proofs, suggesting that exposing undergraduate students to proof methods can develop their conceptual understanding of an underlying theorem.  It is important to note that context can play a large role in mathematical proofs, with a certain proof giving insight for some but not others.  For one of my PhD studies, we aimed to corroborate existing literature to understand whether undergraduate students are aware of the different roles of proof (like explanation) other than just their verifying role – please get in touch if you have any questions using my contact details via the link below.

References

1. Hanna, G. (2000). Proof and its classroom role: A survey. Atas do Encontro de Investigação em Educação Matemática-IX EIEM, 75-104.
2. Rota, G. C. (1997). The phenomenology of mathematical beauty. Synthese, 111, 171–182.
3. Mancosu, P. (2001). Mathematical explanation: Problems and prospects. Topoi, 20(1), 97–117.
4. Hanna, G. (1990). Some pedagogical aspects of proof. Interchange, 21(1), 6–13.
5. Weber, K. (2014). Reflections on justification and proof: Justification and proof in mathematics and mathematics education. Mathematics & Mathematics Education: Searching for Common Ground, 237–257.
6. Hanna, G. (1995). Challenges to the importance of proof. For the Learning of Mathematics, 15(3), 42–49.
7. Weber, K., & Alcock, L. (2004). Semantic and syntactic proof productions. Educational Studies in Mathematics, 56, 209–234.
8. Easdown, D. (2007). The role of proof in mathematics teaching and the plateau
   principle. Proceedings of The Australian Conference on Science and Mathematics Education.
9. Weber, K. (2010). Mathematics majors’ perceptions of conviction, validity, and proof. Mathematical Thinking and Learning, 12(4), 306–336.
10. Weber, K. (2001). Student difficulty in constructing proofs: The need for strategic knowledge. Educational Studies in Mathematics, 48, 101–119.
11. Stylianou, D. A., Blanton, M. L., & Rotou, O. (2015). Undergraduate students’ understanding of proof: Relationships between proof conceptions, beliefs, and classroom experiences with learning proof. International Journal of Research in Undergraduate Mathematics Education, 1, 91–134.
12. Simon, M. A., & Blume, G. W. (1996). Justification in the mathematics classroom: A study of prospective elementary teachers. The Journal of Mathematical Behavior, 15(1), 3–31.
13. Ording, P. (2019). 99 variations on a proof. Princeton University Press.