This blogpost was written by Dr Declan Devlin, an independent researcher with a PhD in Mathematical Cognition. His research focuses on the development of early numerical skills and the cognitive mechanisms underpinning basic numerical processing. Edited by Dr Bethany Woollacott.

In this blogpost, Declan discusses a recent journal article co-authored with colleagues from Loughborough University and KU Leuven (linked at the end of the post). In this article, they aimed to identify the cognitive mechanisms underlying one’s ability to process numerical order. In particular, they investigated the role that familiarity and memory retrieval may play when judging whether number sequences (e.g., 1-2-3) are “in order” or not. In the following, Declan reviews the literature and then describes his recently published research.

Introduction and literature review

To work confidently with symbolic numbers, a child must be able to comprehend both numerical magnitude (cardinality) and relative position within an ordered sequence (ordinality). As an example, this might mean understanding both that (i) six is greater than four and that (ii) five comes after four and before six.

Both cardinality and ordinality are central aspects of numerical development, making them of keen interest to numerical cognition researchers. Researchers often investigate cardinality using magnitude processing tasks which involve making judgements such as “three is greater than two” and “four is less than six”. Similarly, we often investigate ordinality using order processing tasks which involve making judgements such as “1-2-3 is in order” and “2-1-3 is not”.

Both magnitude processing and order processing performance predict mathematical outcomes. However, there is accumulating evidence that order processing is one of the strongest predictors of arithmetic performance, even surpassing magnitude processing^1,2. Moreover, deficits in this order processing capacity are a frequent feature of mathematical learning difficulties, such as developmental dyscalculia^3,4.

In this context, numerical cognition researchers are motivated to understand the cognitive mechanisms and strategies underlying order processing performance. This is because an improved understanding of the mechanisms driving order processing proficiency may lead to the development of more effective screening techniques and targeted interventions for individuals with mathematical learning difficulties.

What drives order processing performance?

A popular approach to investigating the mechanisms underlying order processing is to consider how order is processed differently for different kinds of sequences. For example, when tasked with judging whether sequences are “in order” or not, people tend to be faster at verifying consecutive sequences like 1-2-3 than non-consecutive sequences like 3-5-7^5,6.

Explaining what causes this consecutiveness effect (also known as the “reverse distance effect”) may provide insight into the cognitive mechanisms underlying order processing performance⁷. In this context, two competing explanations of this effect have been proposed, with each implying distinct cognitive mechanisms.

Count-list explanation

The first proposed explanation suggests that children’s early ordinal knowledge is strongly influenced by their repeated exposure to the verbal count-list (“one, two, three, four…” and so on). It is thought that this exposure may lead children to initially believe that “in order” refers only to sequences that directly match the count-list^8,9. Supporting this view, many young children consistently judge non-consecutive sequences as not being in order¹⁰.

Even after learning that non-consecutive sequences can be considered as ordered, both children and adults still process non-consecutive sequences slower than consecutive sequences^11,12. From the count-list perspective, it is thought that non-consecutive sequences are processed slower because they conflict with this early-formed intuition that only count-list sequences are correctly ordered⁹. One could liken this to how early experiences with positive integers continues to impede the processing of negative numbers and fractions even in adults^13,14. For example, our intuitive understanding that 3 is greater than 2 might interfere with our judgement that ¹/₂ is greater than ¹/₃.

Familiarity explanation

Comparatively, the second proposed explanation suggests that order processing is driven primarily by memory-retrieval mechanisms. For example, people may verify “1-2-3” as ordered simply by retrieving this sequence from long-term memory. Under this perspective, the more familiar a sequence is, the easier it can be retrieved from memory. For example, familiar sequences such as 1-2-3 and 2-3-4 are expected to be processed faster than less familiar sequences such as 2-5-8 and 5-7-9. Supporting this view, a recent study found that memory-retrieval strategies were the most common self-reported strategy during an order processing task¹⁵.

In this context, because consecutive sequences are generally more frequently encountered in everyday life than non-consecutive sequences, they are more familiar and thus more easily retrieved from memory. Accordingly, this perspective argues that the consecutiveness effect results from consecutive sequences being processed faster than non-consecutive sequences because they are more familiar and thus more easily retrieved from memory^6,7.

Differentiating between these two explanations

One challenge to differentiating between these two explanations is that they initially appear to make the same prediction: consecutive sequences are predicted to be processed faster than non-consecutive sequences. However, this is not actually the case. Although the count-list perspective does expect consecutive (i.e., count-list) sequences to always be processed faster than non-consecutive (i.e., non-count-list) sequences, the familiarity perspective instead only predicts that familiar sequences will be processed faster than unfamiliar sequences.

Consequently, we can differentiate between these two explanations by considering the processing of familiar but non-count-list sequences such as 2-4-6 and 3-6-9. From the count-list perspective, these sequences are expected to be processed slowly due to not matching the count-list. Whereas, from the familiarity perspective, these sequences are expected to be processed fast due to being highly familiar.

The present study

To differentiate between the familiarity and count-list explanations of the consecutiveness effect, we first needed to isolate familiarity from consecutiveness. To do this, we selected sequences from a previous study in which participants repeatedly compared pairs of sequences on the basis of their familiarity¹⁶. For example, participants were repeatedly asked questions such as “which sequence is more familiar to you, 1-2-3 or 1-3-5?”. This process produced familiarity scores for several sequences, ranging from 0 (least familiar) to 100 (most familiar).

Using these familiarity scores, we then created two versions of an order processing task. The first version included the three most familiar consecutive sequences and the three least familiar non-consecutive sequences (enhanced familiarity condition). The second version included the three least familiar consecutive sequences and the three most familiar non-consecutive sequences (balanced familiarity condition). These sequences are shown in the figure below:

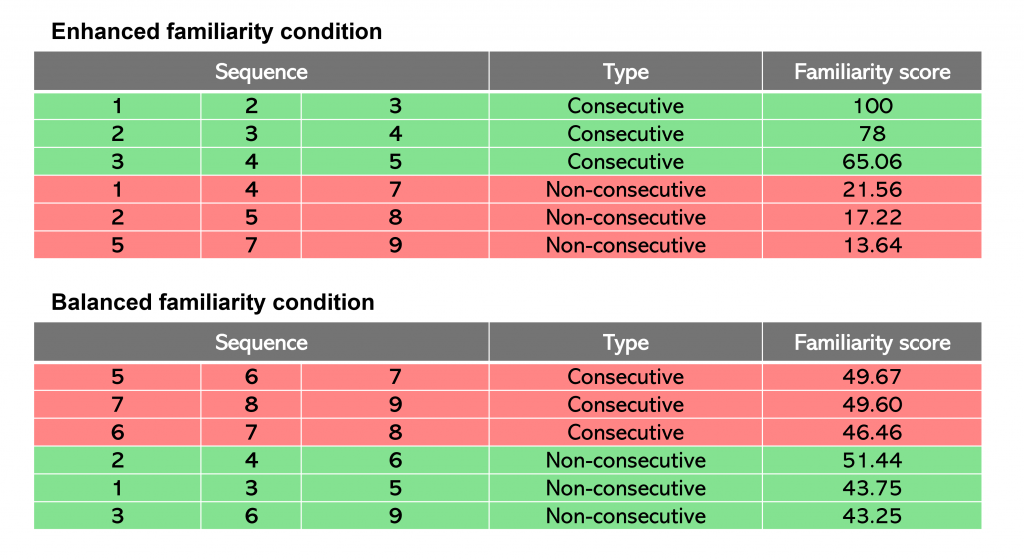
We hypothesised that, if the count-list explanation is correct, the consecutive sequences would be processed faster than the non-consecutive sequences in both conditions. In contrast, if the familiarity explanation is correct, the consecutive sequences would be processed faster in the enhanced familiarity condition, but not in the balanced familiarity condition.

Our findings

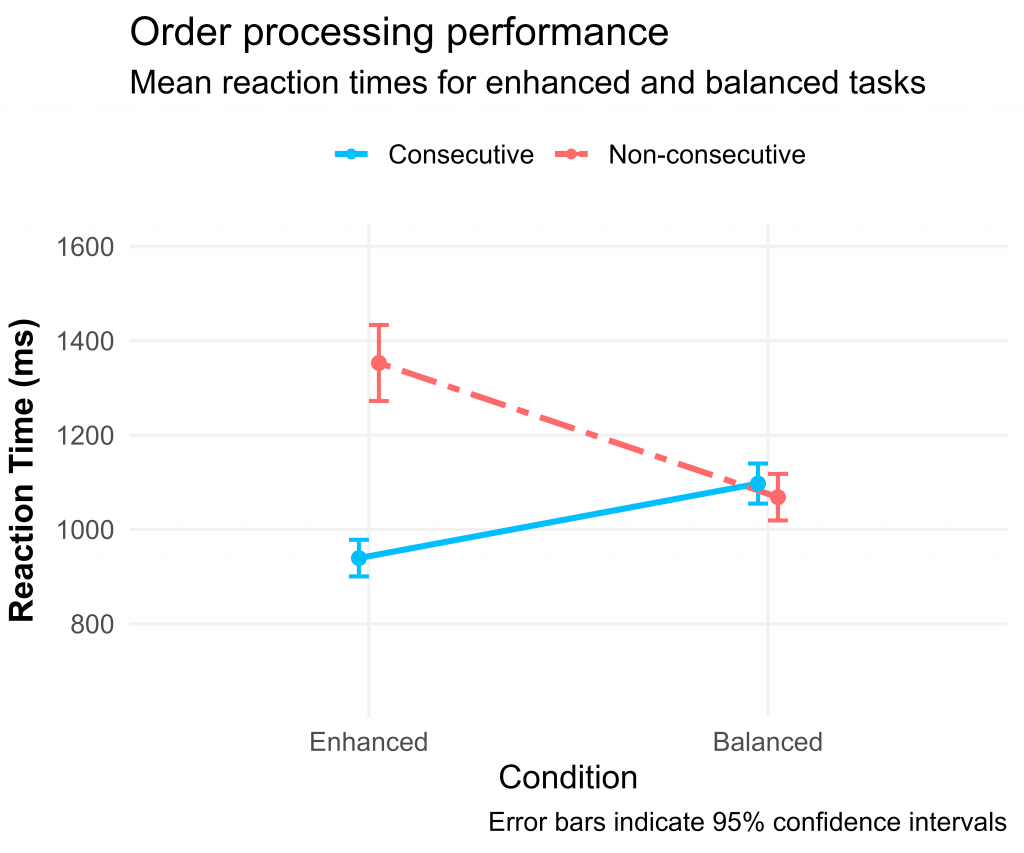
A group of 100 adults completed both versions of the order processing task.

We found that participants processed consecutive sequences faster than non-consecutive sequences in the enhanced familiarity condition, but not in the balanced familiarity condition. This finding is consistent with the familiarity explanation as it suggests that reaction times are influenced more by familiarity than by consecutiveness. These results are visualised below:

Conclusion

The key finding from our study was that consecutive sequences were only processed faster than non-consecutive sequences when they were also more familiar. This suggests that the consecutiveness effect observed in order processing likely results from consecutive sequences being more familiar rather than from their relation to the count-list. Accordingly, this study suggests that familiarity-based memory-retrieval mechanisms likely play a central role in how we process numerical order.

Link to the paper reviewed in this blogpost:

Devlin, D., Moeller, K., Xenidou-Dervou, I.,  Reynvoet, B. & Sella, F. (2025). The presence of the reverse distance effect depends on the familiarity of the sequences being processed. Psychological Research, 89(58). https://doi.org/10.1007/s00426-025-02090-8

References

1. Lyons, I. M., Price, G. R., Vaessen, A., Blomert, L., & Ansari, D. (2014). Numerical predictors of arithmetic success in grades 1–6. Developmental Science, 17(5), 714–726.

2. Sasanguie, D., & Vos, H. (2018). About why there is a shift from cardinal to ordinal processing in the association with arithmetic between first and second grade. Developmental Science, 21(5), e12653.

3. Decarli, G., Sella, F., Lanfranchi, S., Gerotto, G., Gerola, S., Cossu, G., & Zorzi, M. (2023). Severe Developmental Dyscalculia Is Characterized by Core Deficits in Both Symbolic and Nonsymbolic Number Sense. Psychological Science, 34(1), 8–21.

4. Morsanyi, K., van Bers, B. M. C. W., O’Connor, P. A., & McCormack, T. (2018). Developmental Dyscalculia is Characterized by Order Processing Deficits: Evidence from Numerical and Non-Numerical Ordering Tasks. Developmental Neuropsychology, 43(7), 595–621.

5. Lyons, I. M., & Ansari, D. (2015). Numerical order processing in children: From reversing the distance-effect to predicting arithmetic. Mind, Brain, and Education, 9(4), 207–221.

6. Vos, H., Sasanguie, D., Gevers, W., & Reynvoet, B. (2017). The role of general and number-specific order processing in adults’ arithmetic performance. Journal of Cognitive Psychology, 29(4), 469–482.

7. Devlin, D., Moeller, K., Reynvoet, B., & Sella, F. (2022). A critical review of number order judgements and arithmetic: What do order verification tasks actually measure? Cognitive Development, 64, 101262.

8. Hutchison, J. E., Ansari, D., Zheng, S., De Jesus, S., & Lyons, I. M. (2022). Extending ideas of numerical order beyond the count-list from kindergarten to first grade. Cognition, 223, 105019.

9. Gattas, S. U., Bugden, S., & Lyons, I. M. (2021). Rules of order: Evidence for a novel influence on ordinal processing of numbers. Journal of Experimental Psychology: General, 150(10), 2100–2116.

10. Gilmore, C., & Batchelor, S. (2021). Verbal count sequence knowledge underpins numeral order processing in children. Acta Psychologica, 216, 103294.

11. Sella, F., Sasanguie, D., & Reynvoet, B. (2020). Judging the order of numbers relies on familiarity rather than activating the mental number line. Acta Psychologica, 204, 103014.

12. Lyons, I. M., & Beilock, S. L. (2013). Ordinality and the Nature of Symbolic Numbers. Journal of Neuroscience, 33(43), 17052–17061.

13. Obersteiner, A., Van Dooren, W., Van Hoof, J., & Verschaffel, L. (2013). The natural number bias and magnitude representation in fraction comparison by expert mathematicians. Learning and Instruction, 28, 64–72.

14. Vamvakoussi, X., Van Dooren, W., & Verschaffel, L. (2012). Naturally biased? In search for reaction time evidence for a natural number bias in adults. The Journal of Mathematical Behavior, 31(3), 344–355.

15. Dubinkina, N., Sella, F., & Reynvoet, B. (2021). Symbolic Number Ordering and its Underlying Strategies Examined Through Self-Reports. Journal of Cognition, 4(1), 25.

16. Devlin, D., Moeller, K., Xenidou-Dervou, I., Reynvoet, B., & Sella, F. (2024). Familiar Sequences Are Processed Faster Than Unfamiliar Sequences, Even When They Do Not Match the Count-List. Cognitive Science, 48(7), e13481.