The shortcut to mathematics
Written by Dr Jo Eaves and edited by Dr Jayne Pickering. Dr Jo Eaves is a post-doctoral researcher at Nottingham University. She completed her PhD at Loughborough University in 2020. If you are interested in her research and would like to get in touch, please email her directly at Joanne.Eaves2@nottingham.ac.uk
Let’s start with a simple question, what is 6 + 38 – 35?
Now here’s another question; how did you solve it?
Perhaps you used a left-to-right procedure (‘6 + 38 = 44’ and then ‘44 – 35 = 9’)?

Or perhaps you used a ‘shortcut’ strategy of ‘38 – 35 = 3’ and then ‘3 + 6 = 9’? This strategy is known as an associativity shortcut; we can re-order groups of operations and don’t necessarily need to solve them in a left-to-right order. Associativity shortcuts can help students avoid larger numbers or more complex arithmetic, which typically results in quicker and more accurate solutions.
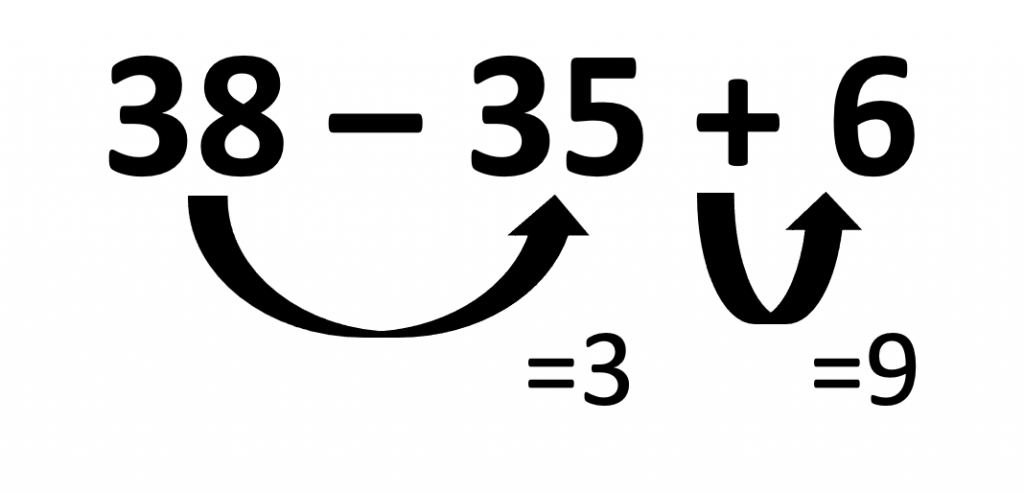
Students often fail to use associativity shortcuts when solving arithmetic problems. Educators have called for this to change, and for individuals’ knowledge and use of arithmetic principles to improve. Improving conceptual understanding and encouraging the flexible use of efficient strategies are the current goals of mathematics education initiatives (Common Core State Standards Initiative 2012; National Mathematics Advisory Panel 2008). My PhD research looked at how people solve arithmetic problems, and how different cognitive skills may contribute to strategy selection.
Over thirteen studies, I investigated whether domain-specific skills (calculation skill and knowledge of the order of operations) and domain-general skills (working memory, inhibition, shifting and visual attention) enable individuals to ‘discover’ the associativity shortcut. I refer to this discovery as strategy ‘identification’, i.e., the “aha” moment you experience when you first find a way for solving a problem. Identification is distinct from strategy execution, which is the process of using the strategy (i.e., calculating an answer). Importantly, the skills underlying strategy identification and strategy execution might be different.
To investigate the role of different cognitive skills in identification, I developed a new tool (called the ‘Identification Analytic’). With this tool, I investigated the cognitive skills involved in arithmetic-strategy use in a precise, theoretically-driven way. The Identification Analytic recorded calculation times to arithmetic problems in real-time. It formed a rolling average which detected when a significant reduction in calculation time occurred. This enabled me to present problems in a naturalistic fashion where students were less aware of my research aims and identify if/when strategy changes occurred.
Thesis findings

In the first part of my thesis, I used the Identification Analytic in four laboratory-based studies; the findings gave rise to three main conclusions. First, students were less likely to identify the shortcut if they misunderstood the order-of-operations acronyms (e.g. BODMAS, BIDMAS, PEMDAS). Some students have an overly rigid interpretation of these acronyms such as a ‘literal interpretation’, where they incorrectly believe that “Addition must be performed before subtraction”, because of the order in which the letters for addition and subtraction appear in the acronym (A before S). Second, students were less likely to identify the shortcut if they had poor inhibition skills.
This means, the ability to withhold making instinctive/default/routinised responses, in a general sense, is important for identifying alternative-solution strategies.
In the second part of my thesis, I investigated whether the use of the associativity shortcut could be encouraged, and if so, how. In seven studies (one laboratory-based and six classroom-based) I investigated whether presenting ‘a + b – c’ problems in more concrete formats (e.g., with plastic counters), self-reporting solution strategies, and solving visually similar but conceptually different problems beforehand (e.g. ‘a + b – b’, ‘a + b – a’), encouraged associativity shortcut use. The main findings were that concrete materials can be helpful and that ‘a + b – b’ problems possess a unique property that bolsters associativity shortcut use. This property could be domain-general (e.g., attention-inhibition) or domain-specific (e.g., strategy-validation); for further discussion of these mechanisms please see https://doi.org/10.1016/j.learninstruc.2019.01.004.
These mechanisms are purely theoretical, but may suggest that asking individuals to pause before they initiate an arithmetic strategy, or helping individuals to validate strategies, is important in encouraging sophisticated strategy use.
The take-home messages for teachers
- The reason a child may not select a strategy is not that they lack an understanding of mathematics per se, but because they lack sufficient cognitive skills (i.e., the ability to withhold making default responses, such as operating left-to-right).
- 75% of adults in my thesis had inadequate knowledge of the order of operations, and approximately 30 – 45% had specific misconceptions that could hinder shortcut use. Misconceptions may constrain the development and application of more sophisticated knowledge.
- When choosing textbooks/worksheets, it may be helpful to pick those that carefully and accurately explain order-of-operation acronyms. Some acronyms explicitly (and incorrectly) say ‘division then multiplication’ and ‘addition then subtraction’ and some advocate a left-to-right approach within those operations.
- It may be helpful to present pupils with a range of ways in which the same problem can be solved to ‘prove’ that different methods are valid and return the same answer.
The take-home messages for researchers
‘Identification’ may be an important, overlooked component of arithmetic strategies. It may be a component that requires domain-specific and domain-general skills, and therefore explain why individuals can fail to use shortcut strategies.
Putting research into the classroom
If you would like to use our associativity-problem sheets in your classroom then please download them from here. If you would like to run your own ‘intervention study’ to try and bolster associative shortcut use, then you can download our research materials from here.
Resources
The materials and arithmetic problems that I have used in undergraduate Psychology classes were published in Eaves, Attridge, and Gilmore (2019) and can be found below.
https://figshare.com/s/230ee9491e0b67d9d3f3
https://figshare.com/s/3b59db4ee96f411cf9e7
https://figshare.com/s/6adad496590c6d713fec
https://figshare.com/s/230ee9491e0b67d9d3f3
https://figshare.com/s/c2b2f174271c7c18e1e6
https://figshare.com/s/7edc99daf2a7588d7d43
https://figshare.com/s/4191d061536fab1b936c
https://figshare.com/s/c3c7ad3aece34ff71aa1
https://figshare.com/s/d5c3fbb77763a9c53778
Glossary
BODMAS: Brackets, Orders, Divisions, Multiplications, Additions and Subtractions.
BIDMAS: Brackets, Indices, Divisions, Multiplications, Additions and Subtractions.
Inhibition: The stopping or overriding of a mental process, in whole or in part, with or without instruction.
PEMDAS: Parentheses, Orders, Divisions, Multiplications, Additions and Subtractions.
Switching: Changing a mental set that has been learned to a new one, which is often interpreted as the ability to shift attention between different tasks.
Visual attention: I refer to as a combination of selective and spatial attention to visual information – i.e., the prioritised processing of relevant information at a relevant location
Working memory: The ability to simultaneously store and process information, which I interpret through the tripartite multicomponent model.
It should be noted that there are many alternative interpretations of these definitions.
Centre for Mathematical Cognition
We write mostly about mathematics education, numerical cognition and general academic life. Our centre’s research is wide-ranging, so there is something for everyone: teachers, researchers and general interest. This blog is managed by Dr Bethany Woollacott, a research associate at the CMC, who edits and typesets all posts. Please email b.woollacott@lboro.ac.uk if you have any feedback or if you would like information about being a guest contributor. We hope you enjoy our blog!