Written by Tom Francome. Tom is a PhD student and a Senior Enterprise Fellow at the CMC at Loughborough University. If you are interested in this blog post and would like to get in touch, please email him directly at T.J.Francome@lboro.ac.uk, or comment below to start a conversation.

How would you teach pupils to measure an angle? What are the steps in the process? Where do learners make mistakes with using a protractor? This article describes the empty protractor: a simple tool that you can use as a replacement for, or as a scaffold towards, a conventional protractor. 

Protractors are used routinely in schools, typically from year five (aged 9-10) onwards. My experience of working with children and the literature suggest that there are several possible misconceptions that can arise around angle measurement.

Learners can get the impression that ‘angle’ means the distance between the two points rather than a measure of turn, so some pupils may perceive this to be larger than that. 

Using a protractor, learners can perceive ‘angle’ as the ‘curved distance’ between points rather than a measure of ‘turn’.^[1]

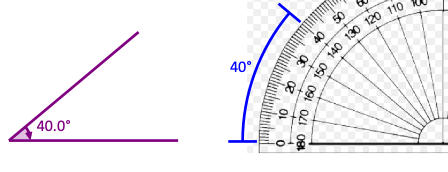
Learners may not position the centre of the protractor on the angle point. 

Learners may not position the line on ‘zero’ or may do so in a way that prevents them from reading the angle. 

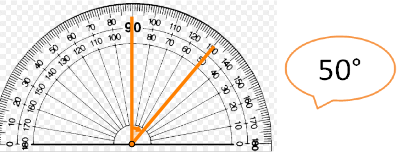
When doing everything else correctly, pupils read the incorrect number off the scale. 

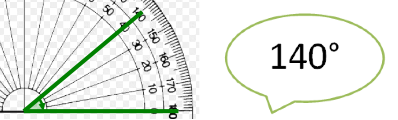
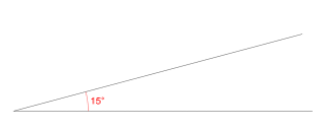
Students often see angle as the distance between the ends of lines^[3]. This may emerge from always seeing examples where both arms are equal length so care should be taken to provide at least some practice where they differ. Students can also learn that bigger arcs, indicating angles, imply bigger angles^[4]. The invariance of the angle can be emphasised by drawing multiple arcs for the same angle and also helps focus on the turn they are to measure. Students can draw lots of 15° angles with different arm lengths and orientations and throw in some 20°and 10° angles for others to find.

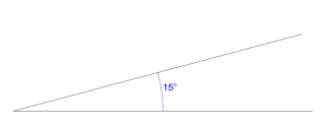
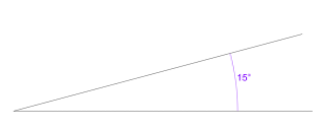
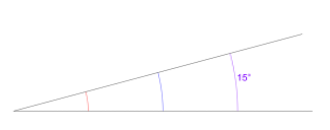
“The use of a protractor is twofold, viz, to lay down an angle or to measure an angle already laid down” (Meredith, 1791). 

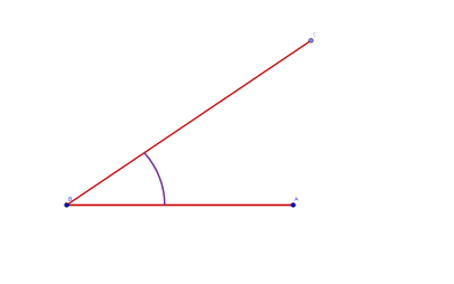
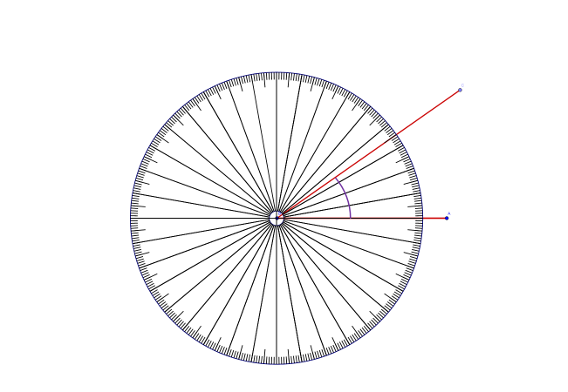
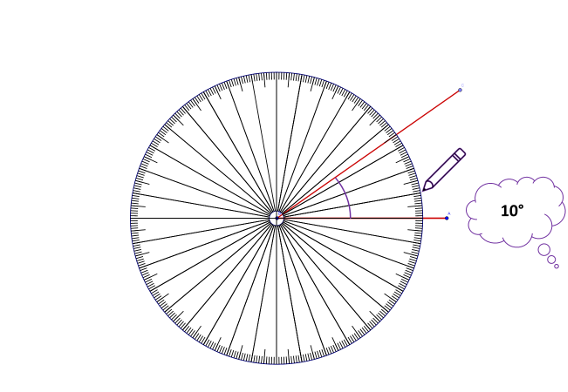
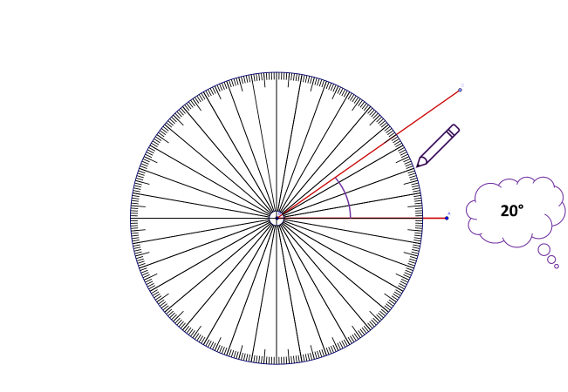
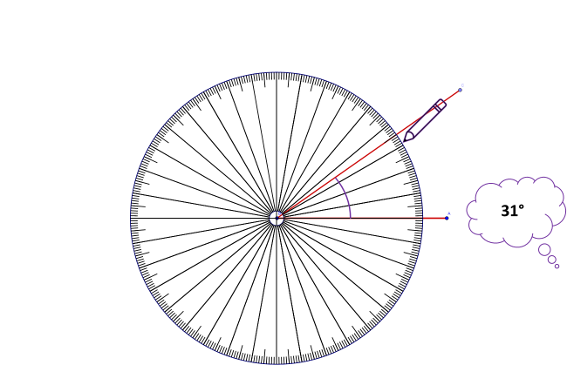
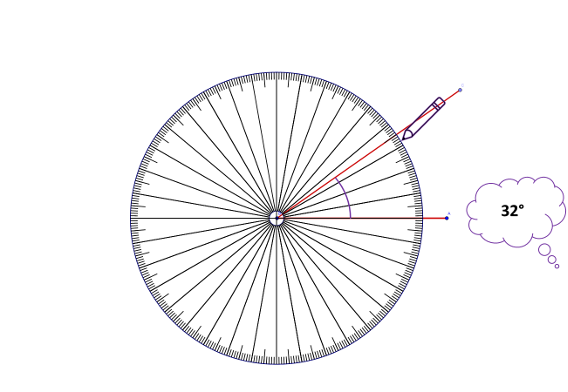
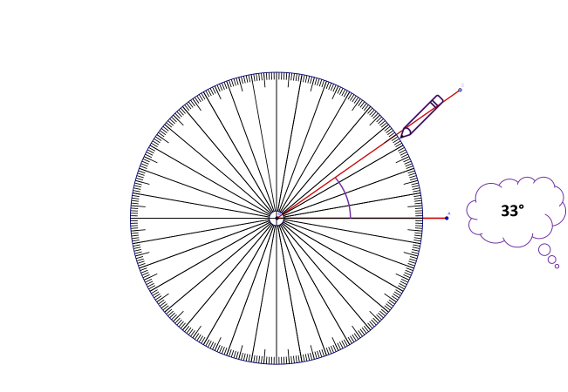
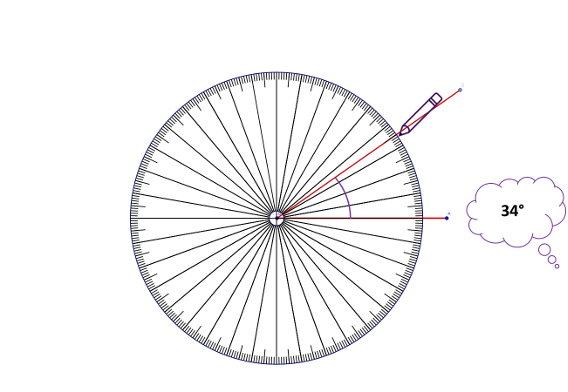
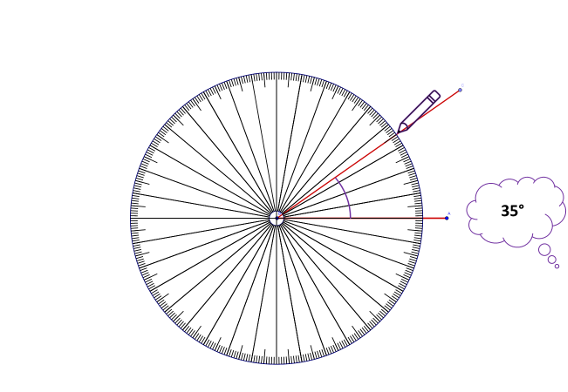
How to measure an angle

1. Place the centre of the protractor on the vertex of the angle. 
2. Place any particular protractor line on top of one angle ray.
3. Count from this line to the other ray^[5].

How to measure an angle:

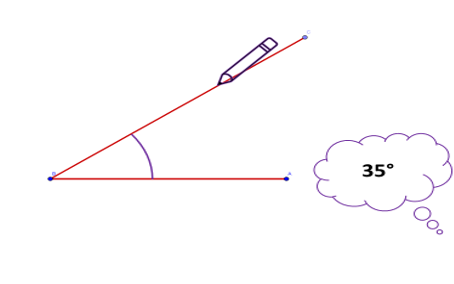
How to draw an angle

1. Draw an initial line (if not given).
2. Place the centre of the protractor on the vertex of the angle.
3. Count the desired angle and mark.
4. Draw a line through the marked point to the vertex.

Rather than a long list of steps to remember, learners only need one; to place the centre at the point of the angle they wish to measure. Learners count the degrees so there is no need to place any particular protractor line on top of the angle line. However, learners quickly conjecture that measuring from one of the angle’s longer lines is easier (although using a pencil to extend the lines (arms) of the angle negates this need). Pupils then count around to the required line. Pupils can draw the turn of the arc, which may be helpful with measuring and understanding angles.

The empty protractor is a simple tool that can help learners develop their conceptual understanding of angles and procedural fluency with measuring and drawing of angles that are crucial for reasoning and problem solving.

Excitingly, if you’d like to try out an empty protractor with your pupils, they are now available to buy alongside some guidance for how to use them and guidance for tasks your pupils can explore whilst developing their expertise with angles.

Here’s a parallel lines task to get you started. As the empty protractor is circular, you can use it to create a circular geoboard and then all the angles will be nice numbers so pupils can measure with confidence.

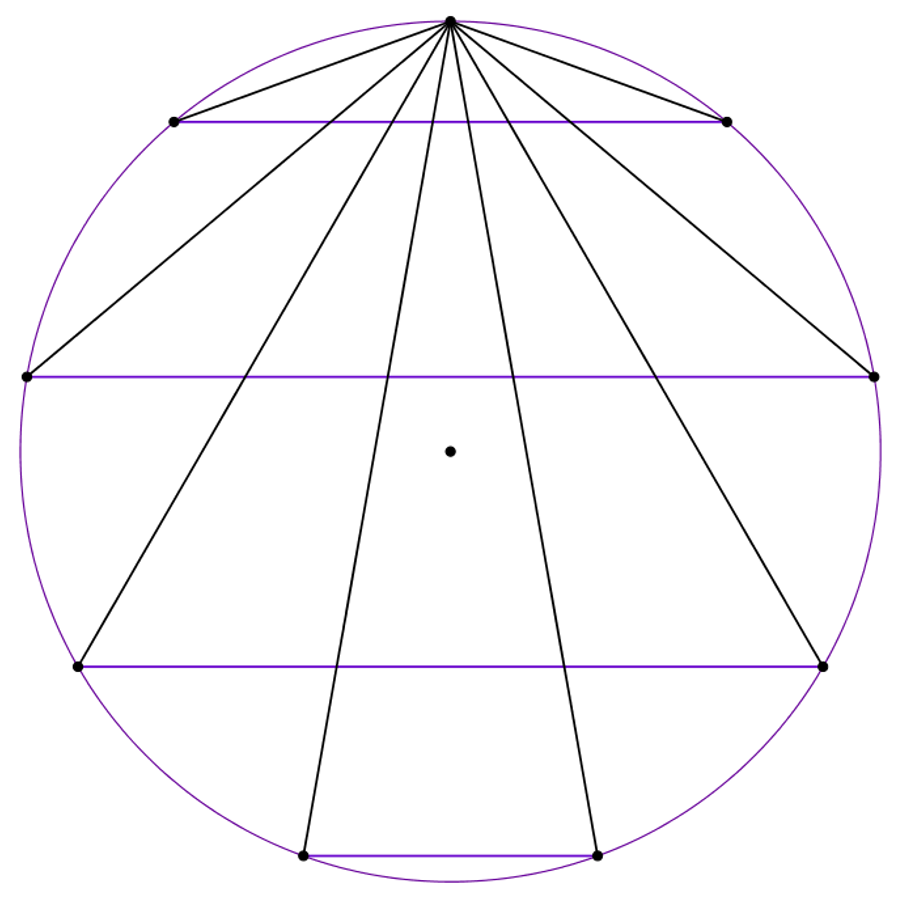
If you mark a point  a point every 40° you create a 9-dot geoboard. The purple line segments in this image are parallel. Work out the angles in the diagram – predict them first. What is the minimum number you would need to measure to know all of the rest?

You can find more tasks for developing thinking about angle in the teacher resources here. Additionally, Jo Morgan collected some other useful resources in a Maths gems post on her excellent Resourceaholic website.

---

^[1] In fact, if the radius is 1 this gives the radian measure of an angle but is hard to do ‘in the field’.

^[2] Francome, T. (2016). Empty Protractor. Mathematics Teaching, 253, 32–33.

^[3] See: DfE (2020) Guidance for teaching mathematics in primary schools available at: https://www.gov.uk/government/publications/teaching-mathematics-in-primary-schools

^[4] See also: Gates, P. and Griffin, P. (1988) Preparing to teach angle, Open University

^[5] Angles can be measured clockwise or anticlockwise on the empty protractor and there are no extra rules about this to be remembered. I have tended to go anticlockwise in the diagrams.

---