Written by Krzysztof Cipora. Krzysztof is a lecturer at Loughborough University. Please see here for more information about Krzysztof and his work. This work is based on an international collaboration with Lilly Roth (University of Tuebingen, Germany), Verena Knoedler (University of Tuebingen, Germany), Stefania Schwarz (University of Tuebingen, Germany), Klaus Willmes (RWTH Aachen, Germany), Jean-Philippe van Dijck (Thomas More University of Applied Sciences and Ghent University, Belgium) and Hans-Christoph Nuerk (University of Tuebingen, Germany).

Generalisation in research

Psychologists make many generalisations when investigating the basic processes underlying numerical cognition. They test a group of participants (a sample) and see whether they observe an effect of interest. If they find an effect, they assume these results generalise to a wider population. The natural question that follows is what constitutes the population and how broadly can we generalise? To people of the same age? People from the same culture? Individuals with a similar level of education? This sample-to-population generalisation is a general principle of cognitive research, but this post will examine it further in relation to the SNARC effect.

SNARC effect

The SNARC effect is the phenomenon whereby people both respond faster to smaller numbers with their left hand and larger numbers with their right hand. This happens even if they are simply pressing one button when the number is odd and the other button when the number is even – i.e., if the task does not explicitly ask about number magnitude. This is thought to relate to a ‘mental number line’ where numbers are ordered from left to right in order of increasing magnitude. This effect may tell us a little about how the brain represents numbers.

Ecological fallacy and other generalisation problems

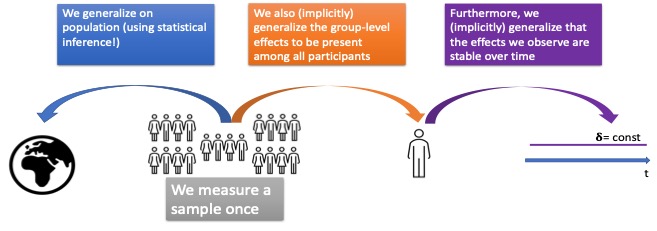
Typically, experiments analyse group effects. That is, the results of one group or condition are compared to the results of another group or condition. Within a group/condition results are averaged together, and researchers do not look at a particular individual’s performance across groups/conditions. If researchers confirm the presence of an effect at the group level, by means of inferential statistics, they make a first generalisation: the effect is likely present in the population. This issue has been the subject of tons of papers, and we will not focus on it. Rather, we will focus on two other generalisations that are very important for theory building – even if they are not always expressed explicitly.

Firstly, theories aimed at explaining general principles of cognition often assume that the group-level effect is present in each individual. This does not necessarily need to be the case, and these unjustified generalisations are called ecological fallacy. Quite often, we find that what is present at the group level, may not adequately represent all the participants. For instance, in SNARC experiments, at the group level we can observe a so-called ‘size effect’ – where it takes longer to respond to large-magnitude numbers than to small-magnitude ones (e.g., to tell whether the number is smaller or larger than ‘5’). Such group differences, in order of milliseconds, can be detected in lab experiments and tell us quite a lot about how humans process information. However, this pattern of responses is reliably present in only 30% of participants, and a reliable reverse pattern (i.e., slower reaction times to smaller numbers) is found in about 10% of individuals (see here). Since the majority of participants do not demonstrate a reliable response pattern, this has serious consequences for how we build a theory of humans’ number representation in general.

The individual prevalence of cognitive phenomena has been intensely investigated in past years. However, even when establishing the individual prevalence of the effect, we still make another generalisation! Namely, we assume that the effect we observed in a given participant is stable. Studies aimed at checking whether this is the case are very scarce, and usually limited to testing the same participants twice. In this project, we decided to go a bit further, and conducted an experiment called Ironman SNARC (named after an exhausting ironman triathlon). Having recruited ten volunteers, we asked them to perform the same task 30 times within 35 consecutive days. This allowed us to check how stable the effect was within the participants and see whether SNARC reflects a stable individual characteristic. The results were really instructive: (1) as expected we observed a robust group-level SNARC effect: the average response times were faster to small / large magnitude numbers when participants responded with their left / right hand respectively, (2) as expected, this pattern of results was not present in all participants, but only 8 out of the 10, (3) there was massive variation in the effects observed in different sessions, (4) when we used our methods, based on bootstrapping approaches to check whether a given participant reveals a reliable effect in a given session, we saw that only one of our 10 participants revealed a reliable effect in more than half of the sessions.

Conclusion

What can we take from this? This study shows that before we generalise, it might be worth checking whether our generalisations are justified. In particular, before we even start thinking about which populations our effects may generalise to (people of a certain education level, culture etc.) it might be worth checking whether our conclusions, based on group-level effects, actually generalise to our sample: to all the tested participants, and to which extent they are stable within our participants. Additionally, each time we wish to consider a cognitive effect as a potential indicator of something (e.g., whether we can use the SNARC effect to predict someone’s level of maths skills), it is worth checking whether the effect we observe is stable across time – it may well be that if we tested the same person on another day, their score would differ dramatically. The Ironman SNARC is still a work in progress, you can see the conference presentation of the preliminary results here. 

Glossary

Ecological fallacy – assuming that a group-level effect is present within a single person, which may be the case, but doesn’t have to be. For instance, a result of a survey showing that British people on average prefer tea (rating it 9 out of 10) over coffee (rating it 7 out of 10) does not imply that every British person prefers tea over coffee. It may well be that there are some individuals, who love coffee and dislike tea, as well as those, who like them equally. We can also imagine a scenario where the majority of participants likes tea and coffee equally strongly (around 8 out of 10), but there is a minority of tea-lovers who rate it 10 out of 10 while strongly disliking coffee (1 out of 10). When averaging across individuals who are indifferent, and the minority of tea-lovers, we would also observe that on average tea is preferred over coffee.

Inferential statistics – infer an effect from a sample to a population, as opposed to descriptive statistics which merely describe the sample you have.

SNARC – Spatial-Numerical Association of Response Codes – a phenomenon whereby participants respond faster to small / large magnitude numbers on the left / right hand side respectively, even if the task does not require them to react to the magnitude (e.g., they are judging whether the number is odd or even).