Written by Dr Ian Jones and Dr Emine Şimşek. Ian is a Reader in Educational Assessment and Head of the Department of Mathematics Education here at Loughborough. His thesis submitted in 2009 proposed a substitution view of the equals sign that is distinct to the more widely reported sameness view. This blog post is a response to recent articles in ZDM that suggested substitution is in fact not so different to sameness after all. Emine is a former member of the CMC whose thesis submitted in 2019 was a comparative study on how textbooks and teachers influence students’ views of the equals sign. She is currently at the Turkish Ministry of Education. Edited by Dr Bethany Woollacott.

We submitted this short note to ZDM (an international mathematics education journal) in response to recent articles they had published. Unfortunately, the journal informed us that they have a policy against publishing responses to articles appearing in their journal, so we are instead posting it here.

Introduction: children’s understanding of the equals sign

It is widely reported that many children view the equals sign (=) as an instruction to perform arithmetic operations and then write down the answer. This is called the “operational” view, and contrasts with viewing the equals sign as meaning the value on the left is the same as the value on the right. This is called the “relational” or “basic relational” view, or as we shall call it here the “sameness” view. The operational/sameness dichotomy is a stable result that has been observed across many contexts and learners (e.g. Şimşek et al.⁵).

Jones and Pratt⁴ proposed a substitutive view of the equals sign that is complementary to and distinct from the sameness view. They defined the substitutive view in terms of interpreting a presented equation as a rule for making substitutions. For example, given i² = –1, then where we encounter i² we can substitute –1, and vice versa.

In a recent issue of ZDM (linked at the end of this blogpost), three articles^1,2,3 considered the substitutive view of the equals sign, arguing to a lesser or greater extent that the substitutive and sameness views are effectively indistinct because the latter necessarily implies the former. Their views conflict with Jones and Pratt⁴ who proposed the substitutive view (i.e., that one side of the equals sign can be replaced by the other) as complementary and distinct to the widely reported sameness view (i.e., that each side has the same value). In the following, we respond by summarising the published evidence in support of the distinctiveness of the sameness and substitutive views of the equals sign, and showing that this evidence withstands the arguments presented across the three ZDM articles. Specifically, differences of opinion about the distinctiveness of the two views seems to derive from how a substitutive view of the equals sign is defined.

Evidence that substitutive and sameness views are distinct

There are three sources of evidence that the sameness and substitutive views are distinct. First, Jones and Pratt⁴ presented a study in which secondary students attempted arithmetic computer puzzles that contained equations, such as 31 = 30 + 1, that could be used to make substitutions of expressions towards a task goal. For example, after selecting 31 = 30 + 1, the students could click any other occurrence of 31 (or 30 + 1) and it changed to 30 + 1 (or 31). Jones and Pratt noticed that students seemed not to be paying attention to sameness when making substitutions to achieve the task goal. They investigated this directly by creating solvable puzzles containing untrue equations, such as 77 = 11 + 33 and other absurdities in the example puzzle shown below, and found that students attended to making substitutions without noticing the lack of sameness.

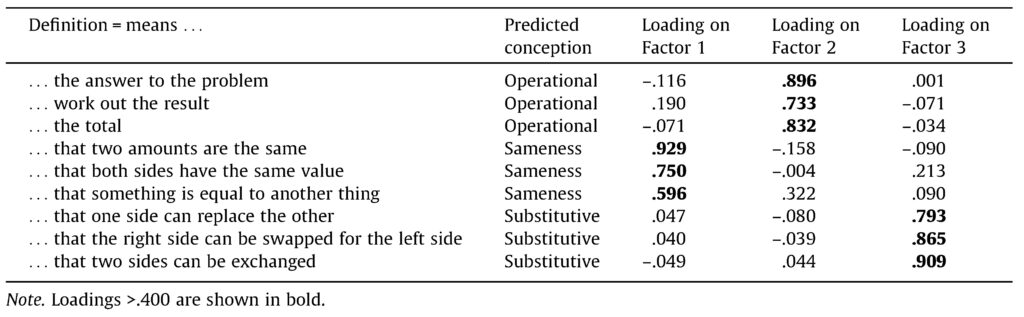
Second, Jones et al.⁶ adapted items from an instrument⁷ in which students rated the ‘cleverness’ of presented definitions of the symbol =. Earlier versions of the instrument contained definitions reflecting an operational view (e.g., “= means the answer to the problem”) or a sameness view (e.g., “= means that both sides have the same value”), and Jones et al.⁶ added definitions reflecting a substitutive view (e.g. “= means that one side can replace the other”). Jones et al.⁶ administered the instrument to students in England and in China, finding that there were three clear views of the equal sign as predicted: operational, sameness and substitutive. They found this result using a Principal Components Analysis which revealed a three-factor solution cleanly reflecting the three views of the equals sign, shown in the table below (taken from Jones et al.^{6, p. 170}).

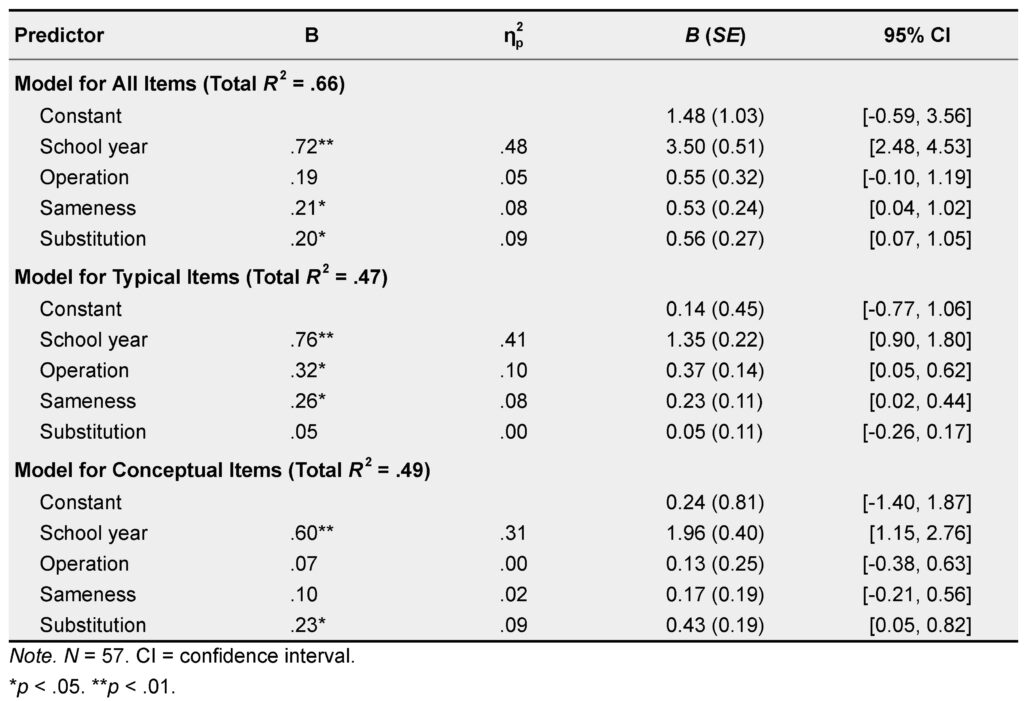
The third piece of evidence showing that the sameness and substitutive views are distinct is that offered by Şimşek et al.⁸. They administered an instrument containing definition items like those described above, as well as algebra items, to secondary students. Some of the algebra items were “typical” of secondary examinations (e.g. “What is the value of y if 5y + 3 = y + 15?”) and some were “conceptual” (e.g. “If e + f = 8 then e + f + g = __”, from Brown et al.⁹). Şimşek et al.⁸ reported that student endorsement of operational and sameness definitions, but not substitutive definitions, predicted performance on the typical items. Conversely, endorsement of substitutive definitions was the sole predictor of performance on the conceptual items. The detailed results are in the table below taken from Şimşek et al.^{8, p.30}. As stated by Donovan et al.³, consistent findings have been independently observed by Szkudlarek et al.¹⁰.

Challenges from the recent ZDM articles

Kieran and Martínez‐Hernández² argued that sameness and substitution are effectively indistinguishable:

“it is precisely because 30 + 1 is the “same” as 31 (i.e., by the addition structure, 30 + 1 = 31, and by symmetry 31 = 30 + 1) that the substitution is tenable. From this perspective, exchanging depends on the support of sameness” (p.1225)

Kieran and Martínez‐Hernández² further stated:

“substitution follows logically from the sameness conception” (p.1136)

Donovan et al.³ agreed:

“substitution does not constitute a wholly different conception of mathematical equivalence but rather logically follows from the sameness conception. That is, two amounts can be swapped or substituted because they represent the same values” (p.1211, italics in original).

It is certainly true that sameness implies substitution, but not that substitution requires sameness. Above we gave the example of 77 = 11 + 33 for which sameness does not hold, and yet Jones and Pratt⁴ reported students replacing 77 with 11 + 33 (and vice versa) in order to solve arithmetic computer puzzles. As Donovan et al.³ put it, “students were able to use the given equations 30 + 7 = 37 and 50 + 8 = 58 as rules for making notational transformations to the expression 37 + 58 without considering the “sameness” of the sides of the equations” (p.1200). We therefore agree with Kieran and Martínez‐Hernández² that “holding a substitutive view without a sameness view is potentially problematic” (p.1136), but this observation supports rather than diminishes the distinctiveness of the two views. Kieran and Martínez‐Hernández² also suggested that “Taking a cue from our students who referred to both truth-value and exchanging with the singular term of ‘sameness”, we suggest that invisible sameness is integral to activity” (italics in original, p.1226). However, as Kieran and Martínez‐Hernández² also pointed out, lack of precise language might lead to students not using terminology regarding exchanging or substituting; but this does not imply that exchanging depends on the support of sameness.

This difference of opinion over the degree of distinctiveness of the substitutive and sameness views resides in how the former is defined. For Kieran and Martínez‐Hernández²,  the substitutive view is independent of the symbol = and instead relates to knowledge of arithmetic facts. So, when a student, Miguel, justified the truth of 7+7+9=14+9 by saying “I did it by adding seven and seven … which is fourteen, the same than there [right side]” (p.1217), Kieran and Martínez‐Hernández² interpreted this as Miguel substituting, or exchanging, 14 for 7 + 7. Donovan et al.³ also followed a definition grounded in knowledge of arithmetic facts rather than in presented equations: “A substitutive view also allows one to replace 21 in the expression 21 + 9 with 11 + 10, because 21 = 11 + 10” (p.1200).

A substitutive definition based on knowledge of arithmetic facts differs from the definition of the substitutive view given by Jones and Pratt⁴: “statements such as i² = –1 can be interpreted as a rule for substitution, namely that i² can be substituted by –1 (and vice versa)” (p.4). According to Jones and Pratt’s⁴ definition, an equation must be presented for there to be a substitutive view of the equals sign, and whether both sides have the same value is strictly speaking irrelevant. Contrastingly, sameness is hardwired into the definitions of substitution provided in the recent ZDM papers. As such, the distinctiveness or otherwise of the substitutive and sameness views – or more precisely the extent to which the former depends on the latter – is a consequence of the definition used.

References

[1] Kieran, C. (2022). The multi-dimensionality of early algebraic thinking: background, overarching dimensions, and new directions. ZDM–Mathematics Education, 54(6), 1131-1150. https://doi.org/10.1007/s11858-022-01435-6

[2] Kieran, C., & Martínez-Hernández, C. (2022). Coordinating invisible and visible sameness within equivalence transformations of numerical equalities by 10-to 12-year-olds in their movement from computational to structural approaches. ZDM–Mathematics Education, 54(6), 1215–1227. https://doi.org/10.1007/s11858-022-01355-5

[3] Donovan, A. M., Stephens, A., Alapala, B., Monday, A., Szkudlarek, E., Alibali, M. W., & Matthews, P. G. (2022). Is a substitute the same? Learning from lessons centering different relational conceptions of the equal sign. ZDM–Mathematics Education, 54(6), 1199–1213. https://doi.org/10.1007/s11858-022-01405-y

[4] Jones, I., & Pratt, D. (2012). A substituting meaning for the equals sign in arithmetic notating tasks. Journal for Research in Mathematics Education, 43(1), 2–33. https://doi.org/10.5951/jresematheduc.43.1.0002  

[5] Şimşek, E., Xenidou-Dervou, I., Hunter, J., Dowens, M. G., Pang, J., Lee, Y., McNeil, N. M., Kirkland, P. K., & Jones, I. (2022). Factors associated with children’s understanding of mathematical equivalence: An investigation across six countries. Journal of Educational Psychology, 114(6), 1359–1379. https://doi.org/10.1037/edu0000747

[6] Jones, I., Inglis, M., Gilmore, C., & Dowens, M. (2012). Substitution and sameness: Two components of a relational conception of the equals sign. Journal of Experimental Child Psychology, 113, 166–176. https://doi.org/10.1016/j.jecp.2012.05.003

[7] Rittle-Johnson, B., Matthews, P., Taylor, R. S., & McEldoon, K. L. (2011). Assessing knowledge of mathematical equivalence: A construct-modeling approach. Journal of Educational Psychology, 103, 85–104. https://doi.org/10.1037/a0021334

[8] Şimşek, E., Xenidou-Dervou, I., Karadeniz, I., & Jones, I. (2019). The conception of substitution of the equals sign plays a unique role in students’ algebra performance. Journal of Numerical Cognition, 5(1), 24–37. https://doi.org/10.5964/jnc.v5i1.147

[9] Brown, M., Hart, K., & Küchemann, D. (1984). Chelsea Diagnostic Mathematics Tests. NFER-Nelson. See http://iccams-maths.org/CSMS/   

[10] Szkudlarek, E., Donovan, A. M., Stephens, A., Alapala, B., Monday, A., Alibali, M. W., & Matthews, P. G. (2021). Children’s equal sign definition endorsement predicts performance on tests of equivalence knowledge. Poster presented at the Society for Research on Child Development Biennial Meeting. (Virtual conference)