Written by Dr Emine Simsek and edited by Dr Ian Jones and Dr Iro Xenidou-Dervou. Emine is a post-doctoral researcher at Loughborough University. Please see here for more information about Emine and her work.

Understanding of Mathematical Equivalence

A useful interpretation of the equals sign for students is thinking of it as a symbol which signifies that the two sides of an equation have the same value and are interchangeable. When solving equations, students are expected to assess the equivalence either by calculating the value on both sides of the equation, or by exploiting arithmetic shortcuts to avoid the need for calculation. Let’s call these shortcuts “relational strategies”. For example, for the following equation “Find the missing number in the equation 64 – __ =  62 – 37”, a relational strategy would be “64 is 2 more than 62, so the answer should be 2 more than 37 which is 39”.

However, research has shown that primary students often view the equals sign only as a “do something symbol” or “the answer to the problem”. They often use incorrect strategies when solving equations that have operations on both sides of the equals sign. Let’s call these strategies “operational strategies”. Two examples of operational strategies used by two Year 5 students are below. 

How can we improve students’ understanding of equivalence? The change-resistance account predicts that too much practice with only a traditional arithmetic format (equations with no operations on the right side, e.g. a + b = c) underpins unwanted incorrect strategies. This tells us that we should vary the problem format in the textbooks and other classroom resources. However, this account was based on research conducted in one country (the USA). Also, it did not account for factors such as teacher knowledge which has been shown to be important to support students’ mathematics achievement. Therefore, to explore what relates to students’ understanding of equivalence, we conducted a study across six different countries (China, England, New Zealand, South Korea, Turkey, and USA).

Our Study

We looked at whether teacher knowledge, the format of equations as presented in textbooks, or both, relate to students’ understanding of equivalence. Participants were Year 4 and Year 5 students (age range 8 to 12, 72% of the participating children were 10 years old) and their teachers across the countries.

We asked students to define the equals sign and to solve equations (e.g. 17 + 28 = _ + 27), and we calculated a performance score for each student. 

We asked teachers to predict correct and incorrect strategies that students might use to solve equations. In teachers’ responses, we looked at whether they were knowledgeable about their students’ use of operational and relational strategies. 

Finally, we asked teachers to provide the names of the current year mathematics textbooks that they used. Then, we analysed the textbooks and identified all the equations involving the equals sign on every other page of the textbooks. We then looked at how many traditional equations and non-traditional equations each textbook has. 

Traditional equations  (no operations beyond the equals sign)	Non-traditional equations (operations/operands beyond the equals sign)
a + b  =  c 58 + 26	a  =  a a  =  b + c a + b  =  c + d

We used an advanced statistical modelling technique to analyse the data collected from 2,760 primary students and 108 teachers.

What we found?

Teachers provided more relational strategies than operational ones. This evidenced that many teachers lack knowledge about students’ use of incorrect (operational) strategies to solve equations. 

In all the countries in the study, the relevant grade textbooks had more traditional than non-traditional equations.

Students’ knowledge of definitions of the equals sign related to their equation-solving performance; students who had more sophisticated knowledge of the equals sign performed better on equations.

The teachers’ knowledge of students’ relational strategies related to the students’ understanding of equivalence but their knowledge of students’ operational strategies did not. From this and based on previous intervention studies, it can be assumed that teachers who are more knowledgeable about (students’) relational strategies support their students’ understanding of equivalence better in the classroom than those who are less knowledgeable of the issue.

We did not find evidence that the format of equations in the current year textbooks influenced students’ understanding of equivalence.

Take-home points for teachers 

• Be aware that many students have an operational understanding of the equals sign and often use only operational strategies to solve equations. 
• Remember that the way students define the equals sign influences their performance in equations. Support your students to define the equals sign relationally.
• Vary the format of equations that students practice in the classroom.
• Encourage use of relational strategies when solving equations. Below is an example of a relational strategy used by a Year 5 student.

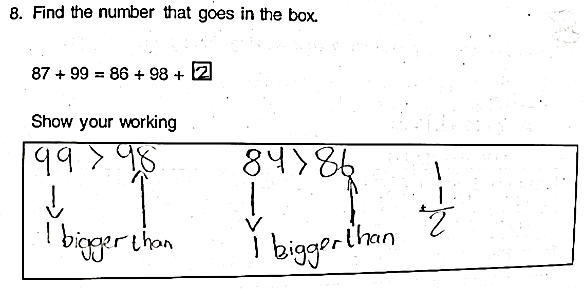
Thank you for reading. Please contact Emine at e.simsek@lboro.ac.uk about ways to improve children’s understanding of mathematical equivalence!

Look out for Emine’s most recent paper, coming soon:

Simsek, E., Xenidou-Dervou, I., Hunter, J., Dowens, M., Pang, J., Lee, Y., McNeil, N., Kirkland, P., Jones, I. (2021). Factors associated with children’s understanding of mathematical equivalence: A cross-cultural investigation across six countries. Submitted for Review.