Garry Barker

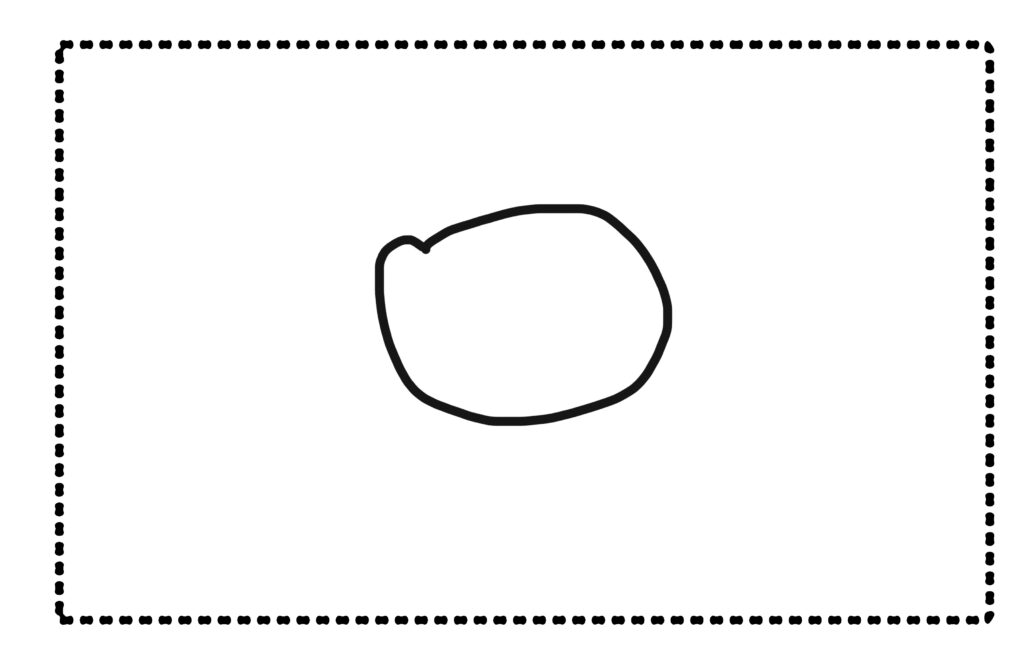
Being faced with the empty vacuum of a clean sheet of paper is something all drawers have to face. The following proposition is a drawer’s response to George Spencer-Brown’s ‘Laws of Form’, written in 1969.

Let the blank page ☐ denote True or False, because it is a space for possibilities to happen and let a ≠ symbol be read as Not or not as things were. I.e. if the blank page is a sort of truth, then once ≠ is added to it, things will have changed, this difference would mean that what was a truth is now something else, it is not true. Conversely if the blank page is in some way false, by adding ≠ to it, it is now something different and if it is not false it can now be true.
Then the primary arithmetic would have the following sentential reading:
If ☐ = false, then ☐ ≠ = not false = true
If ☐ = true, then ☐ ≠ = not true = false

Read in this way the moment before a mark is put on a blank piece of paper is either true or false, however once a mark is put down some sort of truth or falsehood is established and then when a second mark is put down, that first truth or falsehood is questioned, so we now have an untruth or a new truth. 

The ≠ sign symbolises the essence of how we think about ideas, it indicates the capability of differentiating a “this” from “everything else but this.” It represents the drawing of a “distinction”, and can be thought of as signifying the act of drawing a boundary around something, thus separating it from everything else; it also represents that which becomes distinct from everything by drawing a distinction or boundary as well as the crossing from one side of this boundary to the other.

So in effect the first mark we make changes things, we have made a distinction between one thing and another, we have created a difference, and in creating this difference a new possibility is born.

This is reminiscent of another area of theoretical conjecture as to how to visualise the moment of creation itself, that moment of the Big Bang; which as Stephen Hawking has stated, was ‘a quantum fluctuation out of nothing’. In the 1960s John Wheeler and Bryce DeWitt combined quantum mechanics and general relativity into a mathematical framework now known as the Wheeler-DeWitt equation. By integrating Heisenberg’s uncertainty principle into the Wheeler-DeWitt equation He, Gao and Cai have argued that a small empty space can come into existence probabilistically due to fluctuations in what physicists call the metastable false vacuum.
‘When this happens, there are two possibilities. If this bubble of space does not expand rapidly, it disappears again almost instantly, but if the bubble can expand to a large enough size, then a universe is created in a way that is irreversible’. (He, Gao and Cai, 2014)
Perhaps there are very close parallels between the moment of a drawing’s inception and how we think about the coming into being of the universe.

Spencer-Brown takes us into some interesting areas. This is a thought experiment taken from the beginning of the first chapter of ‘Laws of Form’.

Draw a distinction.
Call it the first distinction.
Call the space in which it is drawn the space severed or cloven by the distinction.
Call the parts of the space shaped by the severance or cleft the sides of the distinction or, alternatively, the spaces, states, or contents distinguished by the distinction.
Let any mark, token, or sign be taken in any way with or with regard to the distinction as a signal.
Call the use of any signal its intent. (Spencer-Brown in Farrell, 2010, p. 47) 

Going back to Hawking’s ‘quantum fluctuation out of nothing’, we would have to think about ‘nothing’ as existing infinitely and extended everywhere in every direction. However just to be able to think about this is impossible unless you use a metaphor and in our case it is the empty sheet of paper.

This rectangle represents a blank sheet of paper that itself represents an empty box with no sides that exists infinitely and extends everywhere in every direction. The broken line used to make the rectangle representing an idea that is not solid, or to some extent invisible. This infinitely extended ‘no-thing’ can be mathematically expressed as an empty hyper-set like so: Ø. Within this space we can now make a simple distinction by drawing a line that encircles an area to become a shape.

We now have two spaces, one inside and one outside the shape. The shape in effect is a circumscription of a space. It is though important to remember that what is now inside the shape is actually also the same as but now defined as different from what was circumscribed. Because the original space was infinite the selection would also be infinite.
So a crude mathematical expression of this would be:

If Ø1 represents the original empty hyper-set, then Ø2 could be used to represent the simple distinction or selection and ≠Ø1,2 the boundary that is in effect the common surface between the two spaces that have now been distinguished. We now have three distinguished nothings. A primordial trinity that always includes Ø within it because everything is always composed of what was the original infinitely extended no-thing. This abstract topological construction can now be used as a metaphor for a moment of becoming, of making something from nothing.

This is where mathematics, drawing and religion begin to fuse together. 

Dongshan He, Dongfeng Gao, Qing-yu Cai (2014) Spontaneous creation of the universe from nothing Cornell University Library arXiv:1404.1207v1
http://arxiv.org/abs/1404.1207v1 accessed on 7. 1. 22

Joseph Farrell (2010) Financial Vipers of Venice Port Townsend: Feral House